Задача про меру

[Гость]

Дана последовательность подмножеств отрезка [0,1], мера которых удовлетворяет условию
$\mu(E_n)>\varepsilon>0$
(т.е. больше некоторого числа)
Верно ли что найдётся множество положительной меры, входящее в бесконечное число множеств этой последовательности?

[Сытник Дмитрий]

Что вы иемеете ввиду под словами мера которых --мера каждого из множеств семейства ?

[Гость]

Да

[PAV]

Верно. Рассмотрим множество X, состоящее из всех точек отрезка, входящих в бесконечное число рассматриваемых множеств. Это множество X легко выражается через теоретико-множественные операции следующим образом: $X=\bigcap_{n=1}^\infty \bigcup_{k=n}^\infty E_k$.
Рассмотрим внутренние множества $B_n=\bigcup_{k=n}^\infty E_k$. Это система убывающих вложенных друг в друга множеств, мера каждого из которых не меньше заданного числа $\varepsilon$. В силу известного свойства непрерывности меры отсюда следует, что и мера их предела (т.е. пересечения, т.е. X) не меньше $\varepsilon$.

[Someone]

PAV писал(а):

Верно. Рассмотрим множество X, состоящее из всех точек отрезка, входящих в бесконечное число рассматриваемых множеств. Это множество X легко выражается через теоретико-множественные операции следующим образом: $X=\bigcap_{n=1}^\infty \bigcup_{k=n}^\infty E_k$.

Мне кажется, что это не то множество, которое требуется. Как я понял, речь идёт о существовании такого множества $M$, что $M\subseteq E_k$ для бесконечного множества индексов $k\in\mathbb N$:

Гость писал(а):

Верно ли что найдётся множество положительной меры, входящее в бесконечное число множеств этой последовательности?

Далее будем пользоваться записью чисел отрезка $[0,1]$ в двоичной системе счисления. Некоторые числа имеют две таких записи - одна с периодом $(0)$, другая - с пероиодом $(1)$. Для всех таких чисел, для определённости, будем использовать первую запись, за исключением числа $1$, которое будем записывать как $0,(1)$.

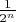
Обозначим $E_k$ множество тех чисел отрезка $[0,1]$, в двоичной записи которых $k$-тая цифра после запятой равна $0$. Тогда $\mu(E_k)=\frac{1}{2}$, в то время как мера пересечения любых $n$ из них равна $\frac{1}{2^n}$. Поэтому никакое множество положительной меры не может содержаться в бесконечном числе этих $E_k$.

Мне только не ясно, можно ли число $\varepsilon>0$ взять сколь угодно близким к единице. Можно попробовать взять множества $_mE_k=\bigcup_{j=mk-m+1}^{mk}E_j$, для которых $\mu(_mE_k)=1-\frac{1}{2^m}$, но мне показалось трудным оценить меру их пересечений. Может быть, я зря испугался.

[незваный гость]

Какая классная задача!

[незваный гость]

Someone писал(а):

Мне только не ясно, можно ли число $\varepsilon>0$ взять сколь угодно близким к единице. Можно попробовать взять множества $_mE_k=\bigcup_{j=mk-m+1}^{mk}E_j$, для которых $\mu(_mE_k)=1-\frac{1}{2^m}$, но мне показалось трудным оценить меру их пересечений. Может быть, я зря испугался.

Мера пересечения $n$ таких множеств - $(1-\frac{1}{2^m})^n$.

Действительно, каждое из них может быть представлено как объединение $2^m-1$ дизъюнктных множеств, каждое из которых имеет меру $\frac{1}{2^m}$ (оно характеризуется цепочкой из $m$ 0 и 1, начинающейся с разряда $mk-m+1$). Пересечение $n$ 'дизъюнктов' имеет меру $\frac{1}{2^{m n}}$, и мы имеем $(2^m-1)^n$ 'дизъюнкта' в пересечении.

[Dan_Te]

Да, можно брать любые $\varepsilon$ сколь угодно близкие к единице. Можно рассмотреть пространство $(\Omega,\mathcal{F})$ с измеримым преобразованием $T\colon\Omega\to\Omega$ и мерой $\mu$, инвариантной и перемешивающей относительно этого преобразования. В качестве множеств $E_k$ рассмотрим $E_k = T^{-k}E_0$, где $\mu (E_0)=1-\varepsilon$.
По определению перемешивания, для любых измеримых множеств А и В верно

$$\lim_{n\to\infty} \mu(A\cap B) = \mu(A)\mu(B)$$

Нетрудно показать, используя это определение, что мера множества, указанного в задаче, должна быть равна нулю.

Someone: в приведенном вами примере, Омега - бесконечные последовательности из нулей и единиц (только вы выкинули из него счетное множество точек); преобразование Т - это сдвиг (или откидывание у последовательности первой координаты); мера - так называемая "мера Бернулли", которая есть не что иное, как распределение последовательности независимых симметричных Бернуллиевских случайных величин. Нетрудно показать, что она является перемешивающей относительно сдвига. Так что в указанном вами примере в качестве E_0 подойдет любое множество меры меньше единицы.