Ещё вопрос о связи хаскелловой нотации с математической: вот дифференциал можно в нотации а-ля Хаскель записать так:

(первый аргумент -- функция, затем точка и приращение аргумента, т.е.

). А как такое записать в математике? Так:

? Но ведь в первом случае функция

каррированная (принимает аргументы "по одному", напр.

-- функция от одного аргумента, полученная частичным применением первых двух аргументов:

и

), а во втором случае -- некаррированная (принимает аргументы сразу, кортежем

).
Я понимаю, что существует изоморфизм между каррированными и некаррированными функциями, но всё же (по-моему) это разные вещи по сути. Наверное и способы записи их "типа" тоже должны отличаться.
(Хотелось бы услышать ответы Xaositect, paha.)-- 15 дек 2010, 18:58 --Почему в математике не принято
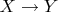
считать множеством всех функций из

и

? Тогда бы обе формы записи были бы корректные, причём первая бы указывала на кар., а вторая не некар. вариант.