На самом деле, Ваше пространство является подпространством индуктивного предела. Ниже я доказываю, что из сходимости в Вашем пространстве следует сходимость в топологии индуктивного предела. Обратно мне доказать не удалось, и как следует из Вашего примера, этого и не должно быть.
Пусть направленность

сходится к нулю в Вашем смысле. Покажем, что она сходится в топологии индуктивного предела. Действительно ,найдется кольцо

. (

-- это то, что в Вашем определении)
По определению индуктивного предела базисом окрестностей в

являются абсолютно выпуклые множества

, такие, что

--окрестность нуля в

.
Берем произвольную окрестность

указанного вида. Поскольку

,найдется такой индекс

, что

при любом

. Пусть теперь

. Множество

открыто в

, не пусто и значит содержит шар

c центром в нуле.
Поскольку мы предположили сходимость в Вашем смысле, начиная с некоторого
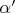
будет

.