Равенство легко следует из формул Коши для коэффициентов ряда. А именно, если

суть окружность

(допустим), обходимая против часовой стрелки, то требуемые коэффициенты равны соответственно

и после подстановки

равенство этих интегралов становится очевидным - их даже легко вычислить. Например, при целом
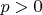
оба интеграла равны коэффициенту в разложении

при

, то есть
