Ваше желание понятно. Но существуют условности устоявшегося языка. И я попробую продемонстрировать, что это очень хорошо.

Вот парочка примеров.
1) Д. Пойа, Математика и правдоподобные рассуждения, с. 40.
Цитата:
Если уравнение

-й степени
имеет
 различных
различных корней
то многочлен, стоящий в его левой части, может быть представлен как произведение

линейных множителей,
2) Э.Артин, Геометрическая алгебра, с. 17-18.
Цитата:
Подмножество

называется независимым, если линейная комбинация
 различных
различных элементов из

является нулевым вектором только в том случае, когда все

. Поэтому, в частности, пустое множество независимо.
Если, читая подобные фразы, Вы полагаете, что область их применимости ограничена условием
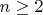
, на том основании, что говорится о
различных элементах, Вы совершаете досадную ошибку. В обоих случаях установившиеся условности математических текстов позволяют без особого напряга трактовать приведенные утверждения не только в случае

, но и в случае

. Во всяком случае, именно такое понимание закладывал в свой текст Э.Артин - как иначе получить из сказанного, что "пустое множество независимо"? Условились уже давно, например, что сумма нулевого числа слагаемых равна 0, что произведение нулевого числа сомножителей равно 1, а сумма одного слагаемого равна ему самому. Что 0 корней – это отсутствие корней и т. д. Что пустое множество, наконец, вопреки происхождению термина от слова "много", вовсе не содержит элементов...
Язык этот сформировался под действием стремления математиков как можно более лаконичными формулировками охватить как можно более общий случай. И сейчас, думаю, вот так никто не пишет:
Цитата:
Если уравнение

-й степени, где
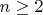
имеет

различных корней
то многочлен, стоящий в его левой части, может быть представлен как произведение

линейных множителей,
если же уравнение 1-й степени имеет корень

, то многочлен, стоящий в его левой части, может быть представлен в виде
P.S. И ещё пример: "Отображение множества

в множество

называется инъекцией, если образы
различных элементов

различны".
А если в множестве

только один элемент, так что
двух различных элементов не найдется, можно это назвать инъекцией? По-Вашему - нет, но математики решили иначе. Если один элемент - это всегда инъекция. Язык у них такой.