Consider the following method of shuffling a deck of
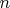
playing cards numbered
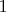
through
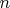
. Take the top card from the deck and then replace it so that it is equally likely to be put under exactly
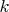
cards for

. Continue doing this operation until the card that was initially on the bottom of the deck is now on top. Then do it one more time and stop.
a) Suppose that at some point there are
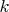
cards beneath the one that was originally on the bottom of the deck. Given this set of
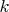
cards explain why each of the possible

orderings is equally likely to be the ordering of the last
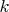
cards
b) Conclude that the final ordering is equally likely to be any of n! orderings
c) Find the expectation ... .