Здравствуйте, хотел бы попросить помочь мне с одним номером по данной теме. Если можете, подскажите, пожалуйста :)
Итак, задание: Решить задачу Коши для уравнения:

Записываю систему уравнений:
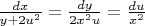
.
Находим ее первые интегралы:
1)

. Откуда

.
2) А вот со вторым первым интегралом проблема :( Подскажите :) Не могу его вычислить.
Пробовал правилом равных дробей, добиться, чтоб было

, но не вышло.