6. (Э.Туркевич) Обозначим через

сумму цифр числа

. Ограничена ли последовательность

?
Ответ: последовательность

неограниченна.
Пусть

. Ясно, что

, когда
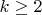
, так что

при

.
С другой стороны,

так что

при
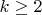
и

. Задача решена.
Замечания.
1. Решение задачи выглядит просто, однако для его получения потребовался месяц работы. Она в своё время довольно долго стояла во Второй школе (её нам сообщил В. А. Сендеров) как «полуоткрытый вопрос», т. е. задача с неясным решением. Немного видоизменив конструкцию, можно показать, что для любого

последовательность

неограничена. Более того,

можно возводить в целую степень

. Для этого надо рассмотреть случаи

и воспользоваться неравенством

(верно также

, равенство достигается когда нет переноса разрядов).
2. Можно показать также, что

при

если

. Это следует из результатов Дж. Бейкера о диофантовых приближениях линейной комбинации логарифмов.
3. Можно построить число

со сколь угодно большой суммой цифр, такое, что

и

. Если же

то либо

, либо

,

. Если

,

, то

.
4. См. также задачу О. Ф. Крыжановского, предложенную на отборе 1994 года команды Москвы (10 класс) на Всероссийскую олимпиаду:
Пусть  имеет все положительные коэффициенты. Может ли многочлен
имеет все положительные коэффициенты. Может ли многочлен  иметь коэффициенты разного знака?
иметь коэффициенты разного знака?