(Оффтоп)
polyedr писал(а):
например,

понял, это у Вас значит на самом деле

polyedr писал(а):
Да, но если принять, например,

, то возможно подобрать такие коэффициенты
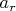
, зависящие от

, что ...
Или я ничего не понимаю, или подбирать

зависящими от

нельзя. Кванторы же


Ну тогда давайте оценим каждую

: возьмем

не зависят от

при

, а интеграл разобьем на 2 кусочка

. Подбираем где

. Первый интеграл

, а второй оцениваем снизу:

и тогда

ну и видим теперь, что при

левая часть растет в зависимости от прочих
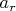
экспоненциально, а правая от них не зависит. Короче говоря, что

, т.е. противоречие. Т.е. Ваша оценка невозможна.
(Оффтоп)
и вообще вместо

лучше было сразу написать
