Это неравенство скорее всего верное. Давайте здесь разберем доказательство автора, если оно не очень громоздкое. Раз специалисты не знают, скорее всего оно ошибочное.
Основной результат - следующая
Теорема 1.
При всех
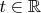
и

, удовлетворяющих условию

, справедлива оценка

, где

- абсолютная константа.
Оценка Теоремы 1 позволяет обычным путем, т.е. используя приближенное функциональное уравнение дзета-функции Римана

в критической полосе (здесь автор ссылается на книгу "Чандрасекхаран К. Арифметические функции. Перев. с англ.- М.: Наука, 1975": стр. 86, формула (53); странно, но этой книги нет в местной библиотеке

), придти к следующему утверждению:
При

справедлива оценка

, где

- любое, а постоянная в символе

зависит только от

. Собственно, это и есть содержание гипотезы Линделёфа.
Доказательство Теоремы 1 занимает 55 страниц, нашпигованных громоздкими формулами. Излагать его здесь - адский труд. Как-то не вдохновляет. Мне кажется, нужно дождаться появления книги в Сети (рано или поздно, все интересное попадает в нее, не правда ли?

), и тогда можно будет устроить brainstorming доказательства.