Заметим, что траектории улиток одинаковы с точностью до поворота на угол

(следует из соображений симметрии). Будем рассматривать движение первой улитки в координатах

(начальные условия

). Тогда движение второй улитки описывается уравнениями

. Условие "погони" первой улитки за второй означает

(1).
Т.к.

и

, то

(2)
откуда

(3),
где

(*).
Условие движения с постоянной скоростью означает

(4).
Итак, имеем систему из двух дифференциальных уравнений (3) и (4).
Выражая

, получаем

. Отбрасывая паразитное положительное значение производной и применяя начальные условия, получим:

(5).
Подставляя это выражение в (3), находим

:

,
откуда (с учетом начальных условий)

(6).
Отсюда легко выразить искомые формулы

и

, однако они получаются громоздкими и ненаглядными.
Гораздо интереснее освободиться от параметра

в выражениях (5) и (6)

и найти зависимость

:

.
Таким образом, улитки движутся по логарифмическим спиралям (подозреваю, что до этого можно было догадаться и исходя из чисто геометрических соображений, используя основное свойство логарифмической спирали о постоянстве угла между касательной к ней и радиусом-вектором, проведенным к точке касания).
Время движения улиток (из (5) и

)

(7),
а расстояние, которое проходит каждая из них,

(8).
При

"догоняемая" улитка помогает "догоняющей" (угол

между векторами их скоростей тупой), при
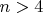
- мешает (

- острый).

- самый интересный случай, т.к.

и

равно расстоянию между догоняющей и догоняемой улитками в начальный момент времени (т.е. стороне правильного многоугольника из условия), поэтому возможен ряд наглядных интерпретаций для описания поведения улиток.