Здравствуйте! у меня 2 задачи про изоморфизм.
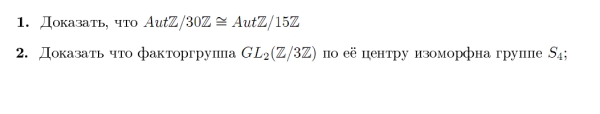
читал разные методичики, есть наработки по решениям, но всё зашло в тупик, помогите разобраться
1 задача.вроде бы разобрался со структурой данных групп.
( группа автоморфизмов = группа возможных отображений группы в неё же. )
В обеих группах бесконечное число элементов, значит изоморфизм может существовать.
Основная идея такая:
пусть f(a1, a2) = (a1*15, a2*15) функция изоморфизма, только её нужно применить к каждой паре из отображения/
есть отображение из a1 в a2, (a1, a2) - элемент первой группы.
Свойство изоморфизма выполняется, f(a1 + b1, a2 + b2) = f(a1, a2) + f(b1, b2), тождественное отображение переходит в тождественное..
в чём ошибка \ неточность? или как правильно построить изоморфизм?
2 задача.разобрался со структурой данных групп.
нашёл центр первой группы:
пермножил две матрицы в прямом и обратном порядке; как и ожидалось, центр - скалярные матрицы.
GL2(Z/3Z) состоит из квадратных матриц 2x2, заполненных числами 0,1,2; при этом их определитель равен +1 или -1 для обратимости.
операции выполняются по модулю 3.
затем я написал небольшую программку, определил количество таких матриц - 24 штуки.
Где-то видел формулу для количества элементов группы GLn(Fm), что-то вроде:
N = 1/(m-1) * (m^n - m)* ... * (m - 1)
по ней количество элементов тоже получилось 24.
к сожалению уже потерял ссылку, и не знаю как доказать(
Затем я посмотрел на S4: это группа перестановок, количество элементов 4! = 24.
Значит изоморфизм может существовать.
в итоге я вижу некое соотношение между тождественной перестановкой и единичной матрицей,
обратной перестановкой и матрицей вращения...
произведение матриц и перестановок тоже чем-то похоже
как связать всё воедино?