
Для любого целого

сумма

где

и

- натуральные числа, не равна

где

натуральное число.
Положим, без ограничения общности дальнейших рассуждений, что

где

-
натуральное число. Тогда сумма

запишется в виде
![$ (u + y)^{n} + y^{n} = u^{n} + nu^{n -
1}y + [n(n - 1)/2]u^{n - 2}y^{2} + \ldots + nuy^{n - 1} + 2y^{n} =
y^{n}( u^{n}/y^{n} + nu^{n - 1}/y^{n - 1} + [n(n - 1)/2]u^{n -
2}/y^{n - 2} + \ldots + nu/y + 2). $ $ (u + y)^{n} + y^{n} = u^{n} + nu^{n -
1}y + [n(n - 1)/2]u^{n - 2}y^{2} + \ldots + nuy^{n - 1} + 2y^{n} =
y^{n}( u^{n}/y^{n} + nu^{n - 1}/y^{n - 1} + [n(n - 1)/2]u^{n -
2}/y^{n - 2} + \ldots + nu/y + 2). $](https://dxdy-03.korotkov.co.uk/f/2/b/8/2b867a1c22b74bd7a00de14822bf527982.png)
Обозначим

Тогда
![$$ x^{n} + y^{n} = (u + y)^{n} + y^{n} = y^{n}(w^{n} + nw^{n - 1} +
[n(n - 1)/2]w^{n - 2} + \ldots + nw + 2) \ne z^{n}. $$ $$ x^{n} + y^{n} = (u + y)^{n} + y^{n} = y^{n}(w^{n} + nw^{n - 1} +
[n(n - 1)/2]w^{n - 2} + \ldots + nw + 2) \ne z^{n}. $$](https://dxdy-04.korotkov.co.uk/f/3/a/8/3a8c065a1adfb5ae2d57a26801c3916a82.png)
Это
утверждение доказывается от противного. Предположим, что многочлен
![$ y^{n}F(w) = y^{n}(w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n -
2} + \ldots + nw + 2) = z^{n} $ $ y^{n}F(w) = y^{n}(w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n -
2} + \ldots + nw + 2) = z^{n} $](https://dxdy-01.korotkov.co.uk/f/c/c/0/cc0b5c717bf7505bea704a52e80d82d382.png)
,
![$ F(w) = w^{n} +
nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2 = z^{n}/y^{n}
= \alpha^{n} $ $ F(w) = w^{n} +
nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2 = z^{n}/y^{n}
= \alpha^{n} $](https://dxdy-03.korotkov.co.uk/f/6/4/b/64b64a704506cddcb4497a7e40c4c39782.png)
где

рациональное положительное число.

для

. Необходимо найти рациональное

, при котором

. Согласно теоремы Бюдана-Фурье и следствия
из него правила (теоремы) Декарта многочлен
![$ F_{\alpha}(w)
= w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2 -
\alpha^{n} $ $ F_{\alpha}(w)
= w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2 -
\alpha^{n} $](https://dxdy-04.korotkov.co.uk/f/b/e/8/be83c87aadcc4da38ea8aeab8ea6b0da82.png)
имеет только один и притом строго
положительный корень, так как

имеет всего лишь одну перемену знаков в системе своих
коэффициентов [1]. Свободный член
![$ 2 - \alpha^{n} < 0,
\alpha
> \sqrt[n]{2} > 1 $ $ 2 - \alpha^{n} < 0,
\alpha
> \sqrt[n]{2} > 1 $](https://dxdy-01.korotkov.co.uk/f/c/b/0/cb017409256e0dbd34070d3674dc867e82.png)
. Подставив, в

значение

, получим

Затем, подставив, в

значение

получим

Так как
![$ \alpha > \sqrt[n]{2} > 1 $ $ \alpha > \sqrt[n]{2} > 1 $](https://dxdy-03.korotkov.co.uk/f/e/9/b/e9b8f816fe35aa7f696d85ae4885c3fe82.png)
, то можно записать

, где

Тогда

.
Значит единственный положительный корень

многочлена

,

не является целым числом и равен

, где

и

- рационально. Подставив

в

, получим

. Представив

в
виде

, где
рациональная величина

, и подставив в
уравнение

, получим уравнение

. Собственно говоря, уравнение для бесконечного спуска
получено. Можно переписать это уравнение в виде

, т.е. замена
(сдвиг)

на

или в более симметричном виде

т.е. замена (сдвиг)

на


Рассмотрим уравнение (*) при

.

После раскрытия скобок и приведения подобных членов получаем

Обозначим

. Далее, обозначим левую часть
(***) через

, т.е.

, а правую часть (***) через

, т.е.

. Функция

есть парабола второго порядка, две ветви которой располагаются симметрично
относительно оси ординат,

и все значения этой функции лежат в верхней полуплоскости, а функция

кубическая парабола. Ясно, что кривые ( графики
функций

и

) на одной и той же плоскости
декартовых координат, где вдоль оси абсцисс, принимая одинаковые значения одновременно, изменяются аргументы

и
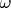
, а вдоль оси ординат отмечаются значения
функций

и

, пересекаются только в одной точке в
первом квадранте (т.е. значения функций

и

в
этой точке пересечения равны,

и значения аргументов

и

равны между собой, т.е.

). В точке пересечения уравнение (***) можно записать в следующем
виде:

Сделав в (i) замену

, получим
уравнение

Дискриминант (ii)

.
Значит уравнение (ii) имеет один действительный корень и два
комплексно-сопряженных корня. Согласно теоремы Бюдана-Фурье и следствия из него правила
(теоремы) Декарта следует, что действительный корень строго
положительный [1]. По хорошо известной формуле для корней
кубического уравнения действительый корень

равен
![$$ \gamma_{0} = \sqrt[3]{\frac{9}{8} + \sqrt{\frac{81}{64}
- 1}} + \sqrt[3]{\frac{9}{8} - \sqrt{\frac{81}{64} - 1}} =
\frac{1}{2}(\sqrt[3]{9 + \sqrt{17}} + \sqrt[3]{9 - \sqrt{17}}) =
2,027279411... (iii) $$ $$ \gamma_{0} = \sqrt[3]{\frac{9}{8} + \sqrt{\frac{81}{64}
- 1}} + \sqrt[3]{\frac{9}{8} - \sqrt{\frac{81}{64} - 1}} =
\frac{1}{2}(\sqrt[3]{9 + \sqrt{17}} + \sqrt[3]{9 - \sqrt{17}}) =
2,027279411... (iii) $$](https://dxdy-04.korotkov.co.uk/f/3/3/7/3376220c5b5a94354588122f8810e9ef82.png)
Исходя из равенств

и

получается, что

Из вышеизложенного вытекает, что в уравнении (***)

является иррациональным числом.

Следовательно последняя низшая ступень
бесконечного спуска уравнения (*), начиная с любого значения

, приводит к выводу, что для любого целого

сумма

где

и

- натуральные числа, не
равна

где

натуральное
число.
С помощью калькулятора в инженерном режиме нетрудно вычислить приближенные значения
иррационального числа

в
(*) для некоторых значений показателя степени

. Здесь ниже
приводятся значения

для

.

.

.

.

.
Наконец сам спуск практически нетрудно построить следующим
образом. Уравнение (*) переписывается в виде


![$$ \beta[(\beta +
\frac{1}{2})^{n - 1} - (\beta - \frac{1}{2})^{n - 1}]+
\frac{1}{2}[(\beta + \frac{1}{2})^{n - 1} + (\beta -
\frac{1}{2})^{n - 1}] = \frac{1}{\epsilon^{n}} $$ $$ \beta[(\beta +
\frac{1}{2})^{n - 1} - (\beta - \frac{1}{2})^{n - 1}]+
\frac{1}{2}[(\beta + \frac{1}{2})^{n - 1} + (\beta -
\frac{1}{2})^{n - 1}] = \frac{1}{\epsilon^{n}} $$](https://dxdy-01.korotkov.co.uk/f/8/1/a/81a27099087cb82ca1623fb81484125a82.png)
![$$ (\beta + \frac{1}{2})^{n - 1} - (\beta - \frac{1}{2})^{n - 1} =
\frac{1}{\beta \epsilon^{n}} - \frac{1}{2\beta}[(\beta +
\frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] ~~~~ (j1) $$ $$ (\beta + \frac{1}{2})^{n - 1} - (\beta - \frac{1}{2})^{n - 1} =
\frac{1}{\beta \epsilon^{n}} - \frac{1}{2\beta}[(\beta +
\frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] ~~~~ (j1) $$](https://dxdy-02.korotkov.co.uk/f/1/4/f/14fed6de786d72f424ac4d48701e531682.png)
С другой стороны из уравнения общего вида (*) можно записать
уравнение для показателя степени


Сравнивая уравнения (j1) и (j2), становится
ясно, что
![$$ \frac{1}{\beta \epsilon^{n}} - \frac{1}{2\beta}[(\beta +
\frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] =
\frac{1}{\epsilon^{n - 1}}, $$ $$ \frac{1}{\beta \epsilon^{n}} - \frac{1}{2\beta}[(\beta +
\frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] =
\frac{1}{\epsilon^{n - 1}}, $$](https://dxdy-02.korotkov.co.uk/f/d/a/f/daf73d895aa8cd0e180537cb34e6223b82.png)
откуда снова получаем
уравнение (j2)

Далее, продолжая аналогичным
образом, спускаясь по лестнице, приходим к уравнению (***).
I. Рассмотрим однородное диофантово уравнение вида

при этом

- целые ,

Постановка задачи - принадлежат ли решения этого уравнения кольцу целых чисел

при различных значениях показателя

[2],[3],[4],[5],[6].
Нетрудно видеть, что уравнение (1) при

имеет целочисленные решения. Например, при
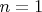
значения

и

а при
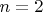
значения

и

удовлетворяют уравнению (1).
Далее утверждается, что уравнение (1) при

не имеет натуральных
решений

, т.е.

.
Доказательство этой старой задачи строится от противного, что и было изложено выше.

II. Далее, если рассматривать (1) для всех целых

, то равенство в (1) возможно только для

. Легко видеть, при

(получается 2 = 1) равенство не выполняется.
Рассмотрим (1) с показателем степени

.

- не равные нулю целые числа.
Нетрудно видеть, что для

равенство имеет место, например, при четных равных друг другу

и

- целое.
При

и, к примеру, при

и

равенство (1) выполняется.
Пусть

, тогда (1) запишется так:

где

.
Ясно, что в (2)

и

.

Пусть

целое, тогда правая часть (3) есть

- ая степень целого числа. Из доказанного выше в разделе I следует, что (3) не имеет целочисленных решений для всех значений показателя степени

и, следовательно, равенство (1) не выполняется для всех

, если

- не равные нулю, целые числа.
III. Пусть в (1) для всех целых

, числа

- рациональные, т.е.

, где

- целые,
не равные нулю, числа.
IV. Пусть в (1) для всех целых

, числа

- иррациональные.
V. Пусть в (1) для
всех целых

, числа

-
комплексные, т.е.

,
где

, а числа

-
вещественные.
Для задач III, IV, V определить условия равенства.
1. Курош А. Г. Курс высшей алгебры. М.: Наука, изд. 9-е, 1968.
2. Эдвардс Г. М. Последняя теорема Ферма. Генетическое введение в
алгебраическую теорию чисел. -М.: МИР, 1980.
3. Куликов Л. Я. Алгебра и теория чисел. -М.: Высшая школа,
1979.
4. Блинов В. Ф. Великая теорема Ферма: Исследование проблемы -М.: Изд-во
ЛКИ,2008.
5. Постников М. М. Теорема Ферма. Введение в теорию алгебраических
чисел. -М.: Наука, 1978.
6. Рибенбойм П. Последняя теорема Ферма для любителей. -М : Мир, 2003.