Только вот в этой теме моя цель показать что пространство во вращающейся системе отсчёта евклидово.
Замечательная цель. Имеем ИСО. Переход во вращающуюся систему отсчета описывается преобразованиями XXX... Вот метрический тензор эффективного трехмерного пространства... Раз Ваша цель
показать что-то - может стоит сразу делать это конструктивно?
Собственно, если Вы не заметили я всё это время ждал Вашего согласия и наконец дождался

В чём здесь криминал?
Да не в чем.
Вот если бы Вы сразу не упрямились, то имели бы возможность весело со всеми посмеяться надо мной.

Вот, что я собирался сделать. За подробным доказательством отослать к книжке Логунова «Лекции по теории относительности и гравитации» пар. 28, 30, стр. 192. Я просто тезисно его здесь изложу.
Метрика пространства при сдвиге в произвольной системе отсчёта тоже должна быть форминвариантна. Вот это условие

Это означает, что при смене положения наблюдателя старая метрика пространства в некоторой системе координат и новая метрика пространства в такой же системе координат должны иметь одинаковую форму. Могут изменится только характеристики системы отсчёта. Математически это означает, что вариация метрики в смысле Ли должна быть равна нулю.

.Отсюда следуют уравнения Киллинга. Их решение даёт конечный результат: скалярная кривизна пространства должна быть постоянна по пространству.

В инерциальной системе отсчёта пространство евклидово, т.е. скалярная кривизна равна нулю
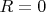
Значит она нулевая и в неинерциальной системе отсчёта.
Но пока Вы myhand думали до меня дошло, что оно не проходит. Так, что извините Алия

- не оправдал….
Поймите меня правильно. Мне не нравится известная метрика пространства не потому, что я не люблю неевклидовую геометрию. Я, например, уверен, что пространство скоростей есть пространство Лобачевского. Но эта метрика пространства получается не как в ОТО. А вот как с обычным физическим пространством?
Как обычно получается метрика пространства в теории относительности. Полагается, что в соседних точках пространства физическое «время» одинаковое.

. (*)
Отсюда

Если бы выражение (*) было полным дифференциалом всё было бы просто замечательно.
И этой темы вообще бы для меня не было. Но это не так и это меня в современной теории не удовлетворяет…
В общем сейчас до меня дошло,

что пространство действительно неевклидовое! Но его надо вводить совсем по другому. Надо использовать обычное координатное преобразование сдвига из вращающейся системы отсчёта



и так как это делается в пространстве скоростей устремить точку
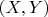
к

.
Тогда сразу получится известный пространственный интервал.
В общем, вывод из всего этого лично для меня такой
геометрия пространства не зависит от того синхронизованы часы или нет.На остальное myhand немного погодя. Пусть у меня немножко это устоится. Сразу на все Ваши вопросы отвечу. Просто мне это уже неинтересно.
