Помогите составить формулу .... (планиметрия)

[VladVlad]

На оси Х находится окружность с радиусом R на расстоянии L от центра.
Их точки А с координатами (0, Н) проведена касательная.
Требуется через заданные параметры выразить угол Х, координаты точки В и длину отрезка АВ.

Заранее всем спасибо!

[gris]

Треугольники подобны. Ещё есть свойство квадрата касательной. Не знаю, поможет ли? Или надо решать через систему координат. А если $R>L$?

[VladVlad]

Я больше 30 лет назад закончил и все уже забыл, а надо для работы сделать расчет, даже как-то перед коллегами неудобно, что не могу рассчитать, кто-нибудь реально может формулу сбацать?

R никогда не может быть больше L.

[gris]

Ну тогда бы я так сделал. Ось $x$ направим влево, $y$ вверх. Касательная изменяется от горизонтального положения до вертикального.

Координаты точки $B(x;\sqrt {R^2-(x-L)^2})\big| x\in [L;L+R)$

Вектор касательной $(-\sqrt {R^2-(x-L)^2}; (x-L))$

Уравнение касательной $(x;\sqrt {R^2-(x-L)^2})+t\cdot(-\sqrt {R^2-(x-L)^2}; (x-L)))=(0;H)$

Найдём t.

Я ничего не напутал?

[vvvv]

Координаты точки В (верхней, т.к. к окружности можно провести еще одну касательную) вычисляются по формуле
см.картинку. Эту формулу нашел Маткад, я только записал систему уравнений

Если координаты точки В известны, то остальное найти уже просто.

[VladVlad]

Добрый вечер уважаемые друзья!
Спасибо всем, кто откликнулся на просьбу. Задача действительно весьма важна для меня, ибо эти формулы должны быть заложены в программу. Попытался я проанализировать ответы. Если честно, то мало что понял. Не потому что я тупой. Я математику знал на 5 да и сейчас многое помню, просто со временем все забывается... Забываются формулы и методика их использования, но здесь я вижу проблему в другом. Я даже не очень понимаю запись формулы, дело в том, что за эти годы многое изменилось, и стиль записи стал совсем другой. А я действительно хочу разобраться в этом вопросе. Например точки с запятой у нас никогда в жизни не было, и я затрудняюсь как ее интерпретировать...

Тов. gris пишет: Координаты точки В ... Как я не ломал голову, но я так и не понял, как получить значения Х и Y, та м в формуле всего одна переменная -Х. Мне нужно две формулы: одна для получения Х, вторая для Y, которая должна содержать стандартные мат. знаки, которые можно запрограммировать: -, +, *, : и тд ...

Аналогичный вопрос и к vvvv: Формула одна, а на выходе два значения, а как их получить? Ведь если подставить туда R, L и H, то на выходе будет только одно значение...

Поясните пожалуйста ...

[gris]

Я просто написал идею, а Вы ушли. Теперь вот завтра докумекую. Идею я понял, просто иногда пишешь пишешь, а автора и след простыл

[mihiv]

Из подобия треугольников $\angle BAO=\angle x$,записываем уравнение

$$\frac {L+\frac R{\cos x}}H=\tg x$$

Отсюда для определения $\cos x$ получаем квадратное уравнение $(L^2+H^2)\cos ^2x+2LR\cos x+R^2-H^2=0$ и $\cos x=\dfrac {-LR+\sqrt {L^2R^2+(H^2-R^2)(H^2+L^2)}}{H^2+L^2}$

[vvvv]

VladVlad в сообщении #324647 писал(а):

Аналогичный вопрос и к vvvv: Формула одна, а на выходе два значения, а как их получить? Ведь если подставить туда R, L и H, то на выходе будет только одно значение...

Поясните пожалуйста ...

В нужно понимать как вектор-столбец.Там 2 координаты х и у .Если Вы подставите конкретные значения
L,H,R , то получите сразу численное значение х и у.

[VladVlad]

Спасибо! Потихоньку пытаюсь разобраться в решении.

Цитата:

Отсюда для определения $\cos x$ получаем квадратное уравнение...

Хотелось понять каким образом? Чтобы выразить тангенс через косинус в формуле должен появиться синус или 2А. Вот формулы.
Каким образом Вы получили данный результат?

[Алексей К.]

mihiv в сообщении #324679 писал(а):

$\cos x=\dfrac {-LR+\sqrt {L^2R^2+(H^2-R^2)(H^2+L^2)}}{H^2+L^2}$

$$\ldots = \dfrac {-LR+H\sqrt {H^2-R^2+L^2}}{H^2+L^2}.$$

[ewert]

Проще всего найти АВ -- это катет в треугольнике АВМ, где М -- центр окружности:

$AB=\sqrt{(\sqrt{L^2+H^2})^2-R^2}$.

Теперь для координат точки $B(x,y)$ просто требуем правильности расстояний до $A$ и до $M$:

$\begin{cases}(x-L)^2+y^2=R^2;\\x^2+(H-y)^2=(AB)^2.\end{cases}$

Эта система сводится к квадратному уравнению (т.к. при вычитании первого из второго получится линейное: $2xL-L^2-2yH+H^2=L^2+H^2-2R^2$); решений будет, естественно, два. Отбираем то, у которого положителен игрек (поэтому выражать лучше икс через игрек, т.е. квадратное уравнение получать для игрека).

[VladVlad]

Большое спасибо, Алексей!
Итак первая нужная величина - угол Х -найдена - ARCCOS от
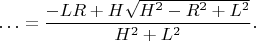
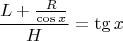
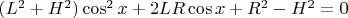
Правда как тов. mihiv из получил для меня так пока и осталось загадкой, если кто сможет пояснить - буду весьма признателен.

Да, вот нашел вторую величину.
Проведем прямую из А в центр окружности (пусть будет точка С)
Из треугольника АОС по т. Пифагора находим АС, далее из треугольника по той же теореме (угол АВС прямой) найдем АВ

Итак, еще одна нужная величина найдена, теперь думаем, как найти последнюю - координаты точки В

Большое спасибо ewert за вышепредоставленный вариант. Я его даже не видел, ибо он вероятно писал его вместе со мной. Отправив свой предыдущий ответ, я увидел и это решение, по-моему это тоже самое, что я сам предложил, только у меня проще выкладки.

[gris]

Точка $B$ находится на высоте $R\sin x$, и на расстоянии $L+R\cos x$ от вертикальной оси.

[VladVlad]

Большое спасибо!
Все нужные значения получены, теперь заложим их в программу.
Ради интереса хотелось бы все-таки разобраться с преобразованиями тов. mihiv - вопрос описан выше