Задача состоит в том, что надо найти такие значения параметра

при котором следующее уравнение имеет один корень :
![$% MathType!Translator!2!1!AMS LaTeX.tdl!TeX -- AMS-LaTeX!
\[
\frac{{x^2 - (3b - 1)x + 2b^2 - 2}}
{{x^2 - 3x - 4}} = 0
\]
% MathType!End!2!1!$ $% MathType!Translator!2!1!AMS LaTeX.tdl!TeX -- AMS-LaTeX!
\[
\frac{{x^2 - (3b - 1)x + 2b^2 - 2}}
{{x^2 - 3x - 4}} = 0
\]
% MathType!End!2!1!$](https://dxdy-01.korotkov.co.uk/f/c/5/0/c50798f42645ee38f3e6412bb310695882.png)
.
Мои соображения таковы: Сначала я нашёл при каких

знаменатель обращается в ноль, а именно в

и

. Далее я рассмотрел числитель и нашёл его дискриминант и приравнял его к нулю,что гарантирует наличие одного корня у данного уравнения.
![$% MathType!Translator!2!1!AMS LaTeX.tdl!TeX -- AMS-LaTeX!
\[
\begin{gathered}
x^2 - (3b - 1)x + 2b^2 - 2 = 0 \hfill \\
D = b^2 - 6b + 9 = (b - 3)^2 = 0 \hfill \\
b = 3. \hfill \\
\end{gathered}
\]
% MathType!End!2!1!
$ $% MathType!Translator!2!1!AMS LaTeX.tdl!TeX -- AMS-LaTeX!
\[
\begin{gathered}
x^2 - (3b - 1)x + 2b^2 - 2 = 0 \hfill \\
D = b^2 - 6b + 9 = (b - 3)^2 = 0 \hfill \\
b = 3. \hfill \\
\end{gathered}
\]
% MathType!End!2!1!
$](https://dxdy-04.korotkov.co.uk/f/7/c/0/7c04f1dd6786270849f21f15fdfc693282.png)
,
но при этом

, корни данного уравнения не должны быть

и

Значит я рассмотрел следующие ограничения:
![$% MathType!Translator!2!1!AMS LaTeX.tdl!TeX -- AMS-LaTeX!
\[
\begin{gathered}
x_1 = \frac{{3b - 1 + b - 3}}
{2} = \frac{{4(b - 1)}}
{2} = 2b - 2 \ne - 1,\,\,\,b \ne \frac{1}
{2} \hfill \\
x_1 = \frac{{3b - 1 - b + 3}}
{2} = \frac{{2b + 2}}
{2} = b + 1 \ne 4,\,\,\,b \ne 3 \hfill \\
\end{gathered}
\]
% MathType!End!2!1!
$ $% MathType!Translator!2!1!AMS LaTeX.tdl!TeX -- AMS-LaTeX!
\[
\begin{gathered}
x_1 = \frac{{3b - 1 + b - 3}}
{2} = \frac{{4(b - 1)}}
{2} = 2b - 2 \ne - 1,\,\,\,b \ne \frac{1}
{2} \hfill \\
x_1 = \frac{{3b - 1 - b + 3}}
{2} = \frac{{2b + 2}}
{2} = b + 1 \ne 4,\,\,\,b \ne 3 \hfill \\
\end{gathered}
\]
% MathType!End!2!1!
$](https://dxdy-02.korotkov.co.uk/f/5/a/c/5ac98293e64516afdcc4d7414f4f69bc82.png)
ну вот значит ответ

, но не так

если подставить параметр в уравнения, то как раз получаем единственный корень
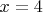
который не подходит по ОДЗ, где я напортачил?
Проверьте пожалуйста!
