байесовская оценка, определение

[g-a-m-m-a]

Не мог бы кто-нибудь сформулировать более или менее четкое определение байесовской оценки?
Заранее спасибо))

[--mS--]

g-a-m-m-a в сообщении #310611 писал(а):

Не мог бы кто-нибудь сформулировать более или менее четкое определение байесовской оценки?
Заранее спасибо))

Без проблем.

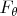
Пусть $\{F_\theta,\ \theta\in\Theta\}$ - некоторое параметрическое семейство распределений. Пусть выполнено условие доминирования относительно некоторой меры $\mu$ на ${\mathbb R}$, т.е. это параметрическое семейство состоит из распределений, абсолютно непрерывных относительно $\mu$. Обозначим через $f_\theta$ плотность распределения $F_\theta$ относительно меры $\mu$.

Пусть параметр $\theta$ является случайной величиной с плотностью $q(t)$ относительно некоторой меры $\lambda$. Функция

$$ f(t,x_1,\ldots,x_n)=f_t(x_1,\ldots,x_n)q(t) $$

является плотностью некоторого распределения в ${\mathbb R}^n\times\Theta$ относительно меры $\mu^n\times\lambda$.
Байесовской оценкой параметра $\theta$, построенной по выборке $X_1, \ldots, X_n$, называется

$$ \theta_n^* = \int\limits_\Theta t q(t|X_1,\ldots,X_n)\lambda(dt), $$

где апостериорная плотность $q(t|x_1,\ldots,x_n)$ параметра $\theta$ вычисляется по формуле

$$ q(t|x_1,\ldots,x_n) = \frac{f_t(x_1\ldots,x_n)q(t)} {\int\limits_\Theta f_s(x_1,\ldots,x_n)q(s)\lambda(ds)}. $$