Функтор банаховой сопряженности и коммутативные диаграммы

[id]

Вопрос, образовавшийся в конце прошлой темы про т-му Дьедонне-Шварца.

Цитата:

То есть никакого основания возможности применить функтор $(^*)$ к коммутативной диаграмме

$$ \xymatrix{ E\ar[r]^T \ar[d]^{pr} & F\\ {E / \mathrm{Ker} \ T} \ar[ur]^{\widehat{T}} } $$

дабы получить диаграмму

$$ \xymatrix{ {E^*} & {F^*} \ar[l]^{T^*} \ar[dl]^{\widehat{T}^*}\\ {(E / \mathrm{Ker} \ T)^* \ar[u]^{pr^*}} } $$

чтобы воспользоваться тем, что ассоциированный оператор $\widehat{T}$ - изоморфизм и сделать отсюда вывод о том, что $\widehat{T} ^*$ - изоморфизм, нет? (это я полагаею, что $\mathrm{Im} \ T$ замкнут и пытаюсь показать замкнутость $\mathrm{Im} \ T^*$)

Пусть дана некоторая коммутативная диаграмма в категории $\mathrm{Ban}$ ( т.е. состоит из банаховых пространств и операторов между ними ). Можно ли подействовать на нее функтором банаховой сопряженности $(^*)$, заменив все пространства на их сопряженные и повернув стрелки?
Что в таком случае можно сказать о результате действия этого функтора на изоморфизмы/мономорфизмы/эпиморфизмы исходной диаграммы? Верно ли, например, то процитированное "рассуждение" выше?

[Padawan]

Можно, на то он и функор - сохраняет композицию

Если $f$ -- изоморфизм, то $f^*$ -- тоже изоморфизм.
Про моно\эпи надо подумать.

-- Вс апр 04, 2010 08:37:52 --

Могу пока только сказать, что если $f^*$ -- моно\эпи, то $f$ -- эпи\моно

[id]

Padawan

Цитата:

Если $f$ -- изоморфизм, то $f^*$ -- тоже изоморфизм.

Обратное вроде как тоже верно.

[Padawan]

Для более конкретного ответа, надо проверить будет ли любая диаграмма $\xymatrix{X^*&Y^*\ar[l]_g }$ образом некоторой диаграммы $\xymatrix{X\ar[r]^f&Y }$, т.е. $g=f^*$.

[id]

Padawan

Цитата:

Для более конкретного ответа, надо проверить будет ли любая диаграмма $\xymatrix{X^*&Y^*\ar[l]_g }$ образом некоторой диаграммы $\xymatrix{X\ar[r]^f&Y }$, т.е. $g=f^*$.

Тут $X^*$ - просто обозначение для элемента диаграммы - или же именно что банахово сопряженное к $X$? Ведь, скажем, в первом случае "можно взять" $X^* = C[a,b]$ и такая диаграмма образом не будет уж никак.

[Padawan]

Именно банахово сопряжение

-- Вс апр 04, 2010 09:22:00 --

id в сообщении #306237 писал(а):

Padawan

Цитата:

Если $f$ -- изоморфизм, то $f^*$ -- тоже изоморфизм.

Обратное вроде как тоже верно.

А как? Вот в мою сторону понятно: допустим $f$ - изо, тогда, для некоторого $g$ имеет место КД

$$ \xymatrix{X\ar@(ul,dl)[]_{1_X}\ar@<0.5ex>[r]^f&Y\ar@(ur,dr)[]^{1_Y}\ar@<0.5ex>[l]^g} $$

Сопряжение превратит эту диаграмму в

$$ \xymatrix{X^*\ar@(dl,ul)[]^{1_{X^*}}\ar@<-0.5ex>[r]_{g^*}&Y^*\ar@(dr,ur)[]_{1_{Y^*}}\ar@<-0.5ex>[l]_{f^*}} $$

так как $(1_X)^*=1_{X^*}$ и $(1_Y)^*=1_{Y^*}$. Значит, $f^*$ -- тоже изо.

А как в обратную сторону сделать без ответа на сформулированный мной вопрос - не знаю.

-- Вс апр 04, 2010 09:45:07 --

Предположение: если $X$ и $Y$ - рефлексивные пространства, то для любого $g\colon Y^*\to X^*$ найдется $f\colon X\to Y$ такое, что $g=f^*$.

[id]

Padawan
Последовательность $(\mathcal E)$ в $\mathrm {Ban}$ точна $\Leftrightarrow$ её сопряженная последовательность $(\mathcal E^*)$ точна . (это из "Лекций ..." Хелемского, Гл. 2 пар. 5)

$T$ - топологический изоморфизм $\Leftrightarrow$ последовательность

$$ \xymatrix{ \dots 0 \ar[r] & 0 \ar[r] & E \ar[r]^T & F \ar[r] & 0 \ar[r] & 0 \ar[r] & \dots}$$

точна.

[Padawan]

Пусть $A\colon X\to Y$. Будет ли $\operatorname{Im} A^*=\{\varphi\in X^*:\operatorname{Ker}\varphi\supset \operatorname{Ker} A\}$ ?

[id]

Padawan
Если $\mathrm{Im} \ A$ замкнут, то,кажется, да: Данфорд-Шварц, том I, глава VI, параграф 6 "Операторы с замкнутой областью значений", Теорема 2.

Если нет... видимо, можно придумать контрпример.

-- Вс апр 04, 2010 20:12:24 --

Хм, может быть диагональный оператор $T_{\lambda}: l_2 \to l_2$ с $\lambda \in c_0$, все компоненты которого ненулевые? Ядро тривиально.
Ну и специально подобрать функционал $y$ из $l_2$, чтобы $\{\frac {y_i} {\lambda_i}\}_i$ не была квадратично суммируемой?

[Padawan]

id в сообщении #306358 писал(а):

Padawan
Если $\mathrm{Im} \ A$ замкнут, то,кажется, да

Так я и думал :)

[id]

Цитата:

Для более конкретного ответа, надо проверить будет ли любая диаграмма $\xymatrix{X^*&Y^*\ar[l]_g }$ образом некоторой диаграммы $\xymatrix{X\ar[r]^f&Y }$, т.е. $g=f^*$.

Цитата:

Теорема 3.
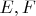
Пусть $E, F$ - нормированные пр-ва, $S: F^* \to E^*$-ограниченный лин. оператор. $S = T^*$ для некоторого ограниченного линейного оператора $T$ $\Leftrightarrow$ $S$ непрерывен относительно слабых* топологий в $F^*$ и $E^*$.

Это из того же Хелемского.
Ну а еще к тому же слабая и слабая* топологии совпадают для рефлексивного пространства, и линейный ограниченный оператор непрерывен относительно слабых топологий, что автоматически дает предложение выше.

-- Пн апр 05, 2010 17:00:35 --

Пожалуй, не слишком это хорошая была мысль пытаться доказывать тот факт подобным образом, куча неприятных моментов с насилием над обозначениями.

В самом начале, кажется, должна стоять диаграмма

$$ \xymatrix{ E\ar[r]^T \ar[d]^{pr} & {\mathrm{Im} \ T} \ar[r]^{in} &F\\ {E / \mathrm{Ker} \ T} \ar[ur]^{\widehat{T}} } $$

для которой нам известно, что $\widehat{T}$ - изоморфизм.
"Сопряженная" к ней будет

$$\xymatrix{{E^*} & {({\mathrm{Im} \ T})^*} \ar[l]^{T^*} \ar[dl]^{\widehat{T}^*} & {F^*} \ar[l]^{{in}^*}\\{(E / \mathrm{Ker} \ T)^* \ar[u]^{pr^*}} }$$

Идея была в том, что если показать то, что ассоциированный оператор к $T^*$ - изоморфизм банаховых пр-в, то все доказано.
При этом нас вообще-то говоря не очень интересует $({\mathrm{Im} \ T})^*$,${\widehat{T}}^*$ и $(E / \mathrm{Ker} \ T)^*$, т.е. надо бы показать, что
1) $(\mathrm{Im} \ T)^*$ топологически изоморфно $F^* / \mathrm{Ker} \ T^* $
2) $(E / \mathrm{Ker} \ T)^*$ топологически изоморфно $\mathrm{Im} \ T^*$
3) $\widehat{T} ^*$ эквивалентен $\widehat{T^*}$
4) Образ $\mathrm{pr}^*$ - замкнут. (Хотя это вроде и так ясно, ибо $(E / \mathrm{Ker} \ T)^*$ банахово, а $\mathrm{pr}^*$ - изометрический оператор).

Хм, и как бы это дело все показать?

[Padawan]

Значит для рефлексивных пространств функтор сопряжения полную симметрию осуществляет:
$f$ - эпи/моно $\Leftrightarrow$ $f^*$ моно/эпи и т.д.

Так как он полный и верный, т.е. если $f\neq g$, то $f^*\neq g^*$ - это вообще в любых нормированных (лишь бы теорема Хана-Банаха была верна).