Ноги этого запутанного вопроса, растут из другой известной Вам темы
http://dxdy.ru/topic31438.html:
Cгруппируем выборку малых множителей

.

.
По предварительному условию число

делит

. В этом случае

,

и

не сравнимы с нулем, поскольку сравнение

или

вместе со сравнением

противоречило бы требованию ВТФ (взаимной простоты чисел

). Этот же вывод можно сделать и так: поскольку

не делит ни

, ни

, то

должно делить

, так как

.
Когда число

имеет вид

то, при Случае 1 ВТФ

. Одно из слагаемых сравнимо с 0 из-за особенных свойств числа

. Но в подслучае Случая 2, который был упомянут с разъяснениями к нему, у меня продолжаются сомнения, несмотря на то, что Вами он был (при беглом просмотре) принят.
Далее мы перекинулись на Случай 1, который увёл в сторону от проблемы мои сомнения, учитывая, что он легко объясняет сравнимость с нулем трех слагаемых, что радовало душу.
Но сомнения снова вернулись.
(Хотя по модулю

число

является кубом какого-то числа непременно -
если это поможет разобраться).
Поэтому и открыл эту тему, чтобы издалека понять и разобраться "что к чему" и распутать этот запутанный случай.
В общем-то вопрос можно и так поставить:
Есть ли гипотетический модуль

, который не делит (

) и делит
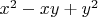
, случай, когда

≢

.
Нету, потому что см.выше.
Таким образом, рассмотрен вопрос, что, если

не делит (

), то есть выполняется

≢

в этом случае:
a)

≢

b)

≢

и, соответствено,

≢

, а значит ситуацию для

можно не рассматривать,
если

не делит (

), то есть выполняется

≢

,
т.к. она противоречит условию

и тогда, аргументы, выдвинутые для возможности (справедливости):

, что существует единственно возможное решение только, когда

,
являются верными и единственными в защиту этого вывода. (Тогда можно не латать доказательство для подслучая 2 Случая 2.)
Однако, если такой вывод верен, то возможно следующее:


Предположив, что

, получается, что

Это, вроде, не противоречит предыдущему выводу, т.к.

Однако - пример, для случая

и

:

Что невозможно, т.к. это вообще ошибка в предположении. Так?