помогите найти интеграл

[Lyudmilka]

интеграл от sqrt(1+36/x^4)

-- Пт мар 26, 2010 05:26:08 --

пробовала решить заменой 6/x^2=tg t. Получается громоздкое подынтегральное выражение, которое, на мой взгляд, совсем не разрешимо.

[Lyudmilka]

$$\int_{2}^{6} \sqrt{1+\frac {36} {x^4}} dx$$

[AD]

Это "дифференциальный бином", про него всё известно.
(Первая ссылка в гугле)

[Lyudmilka]

Я тоже сначала так думала. Но p=1/2 - не целое; $\frac {m+1} {n}$ = (0+1)/(-4)=-1/4 - не целое; $\frac {m+1} {n}$+p = -1/4+1/2=1/4 - тоже не целое. Этот метод не подходит

[AD]

А Вы почитайте повнимательнее ссылочку/учебничек. Этот метод этим и знаменит, что если он не подходит, то ничто не подходит.

[Lyudmilka]

У меня основное задание - решить криволинейный интеграл. Не могу же я дать ответ - нет ответа

-- Пт мар 26, 2010 10:13:28 --

$$\int_{AB}3xyds$$

от точки А до точки В по параболе xy=6

Здесь я делаю подстановки: y=6/x,

$$ds=\sqrt{1+y'^2} $$

Получаю этот интеграл:

$$\int_{2}^{6} \sqrt{1+\frac {36} {x^4}} dx$$

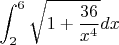
Правильно? И теперь в ответе - интеграл не разрешим? Так же не должно быть в контрольной

-- Пт мар 26, 2010 10:29:17 --

Этот интеграл нельзя выразить через элементарные функции. А по другому нельзя?

[Полосин]

Lyudmilka в сообщении #302590 писал(а):

по параболе xy=6

Неужели в задании так и написано? Тогда это неправильные пчёлы. Они делают неправильный мёд.

[AKM]

Lyudmilka в сообщении #302590 писал(а):

... от точки А до точки В по параболе xy=6

................................................

Так же не должно быть в контрольной.

Ну, если в контрольной гиперболу $xy=6$ обозвали параболой, то возможны и другие недоразумения.

Интегралы не решают. Их берут, вычисляют, находят, --- но только не решают.
Решают, например, задачи на вычисление интеграла.