Теорема Жордана via непланарность K_3,3

[id]

Просматривал доказательство теоремы Жордана (которая про замкнутую кривую и несвязность дополнения) из "Элементов комбинаторной и дифференциальной топологии" Прасолова, заметил странный момент в одной из Лемм. А именно...

(Жордановой кривой называется образ $S^1$ при непрерывном инъективном отображении $f: S^1 \to \mathbb R^2$)

Цитата:

Лемма:
Если $C$ - жорданова кривая, то $\mathbb R^2 \setminus C$ не является линейно связным.

Д о к а з а т е л ь с т в о. Проведём к кривой $C$ опорные прямые и вы-
берем на них точки $A_1$ и $A_2$ , лежащие на кривой $C$. На двух дугах кри-
вой $C$, заданных точками $A_1$ и $A_2$ , можно выбрать точки $B_1$ и $B_2$ так,
что отрезок $[B_1, B_2]$ не будет пересекать кривую $C$ (рис. 35); действительно,
каждая из этих двух дуг является компактным множеством, поэтому пере-
сечение дуги с любой прямой, параллельной опорным прямым, компактно.
На отрезке $[B_1,B_2]$ выберем точку $A_3$ . Если бы точки $A_3$ и $B_3$ можно
было бы соединить путём, не пересекающим кривую $C$, то мы получили
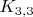
бы вложение графа $K_{3,3}$ в плоскость, чего не может быть.

Ну допустим понятно, что подразумевалось "внутренность отрезка не будет пересекать кривую...", "выберем на интервале $(B_1,B_2)$..."; но не вполне понятно, почему точки $B_1, B_2$ вообще можно выбрать - и тем более такими тривиальными аргументами.

Я попробовал доказать это, выбирая нужные точки в близости к $A_1$, рассматривал пересечение её окрестностей с кривой минус линейно связная компонента точки $A_1$ при этом пересечении, замыкал все это дело, получал убывающую последовательность компактов с пустым пересечением, а отсюда - пустоту некоторого конечного пересечения. Но точка $A_1$ может не быть изолированной, при этом не лежать на некотором отрезке (канторово мн-во пусть, допустим, будет в пересечении $C$ с левой вертикальной прямой), поэтому подобные тривиальности опять же не проходят.

Собственно... как же это легко доказывается?

[ewert]

не вникал, но мне почему-то показалось, что дополнение до компакта открыто -- и, следовательно, состоит из интервалов. Вот на границах одного из этих интервалов и возьмём.
(Пардон за легкомыслие, если что не так.)

[id]

Да, очень похоже на то. Вопрос, видимо, закрыт.

Спасибо!