Преобразовать задачу ЛП к каноническому виду

[Sega611]

Здравствуйте. Правильно ли я преобразовал задачу линейного программирования к каноническому виду?
Задача:
$Z=\sum \limits _{i=1}^{5} {c_ix_i}\to max$
$\sum \limits _{j=1}^{5} {a_i_jx_j}\leqslant b_i$, $i=1,2$
$\sum \limits _{j=1}^{5} {a_i_jx_j}\geqslant b_i$, $i=3,...,8$
$\sum \limits _{j=1}^{5} {a_i_jx_j}= b_i$, $i=9,10$
$x_j\geqslant 0$, $j=1,2$
Канонический вид:
$Z=(-1)\sum \limits _{i=1}^{5} {c_ix_i}\to min$
$\sum \limits _{j=1}^{5} {a_i_jx_j}+x_6=b_i$, $i=1,2$
$\sum \limits _{j=1}^{5} {a_i_jx_j}-x_7=b_i$, $i=3,...,8$
$\sum \limits _{j=1}^{5} {a_i_jx_j}= b_i$, $i=9,10$
$x_j\geqslant 0$, $j=1,2,6,7$
$x_j=y_j'-y_j''$, $y_j'\geqslant y_j''\geqslant 0$, $j=3,...,5$

[Yu_K]

Последнее нер-во я бы разбил на два (а то получается у вас $x_i , i=3,4,5$ будут только неотрицательными).

[Sega611]

А разве не все переменные в каноническом виде должны быть неотрицательны?

[Yu_K]

Вот именно, что все должны быть неотрицательны. Поэтому нужно заменить часть исходных переменных (те которые могут быть отрицательными) на разность двух новых, которые уже будут неотрицательны - что Вы и сделали. Но при этом последнее ваше двойное неравенство "отбросило" часть допустимой области - что не есть "хорошо". И еще желательно всю систему переписать в новых переменных, которых будет всего $2+2+3 \cdot 2$.

[Zealint]

Абсолютно неправильное решение.
У Вас ограничений типа "меньше либо равно" 2 шт., значит там должны появиться 2 переменные,
ограничений типа "больше либо равно" 6 шт., поэтому там должны появиться ещё 6 переменных.
Переменные, которые не имеют ограничений Вы правильно разбили, но как правильно же Вам указал предыдущий автор, их надо включить в саму задачу.

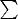
Мне кажется (ИМХО), надо переписать все без значков $\sum$, а аккуратно все выписать по переменным.

[Yu_K]

Только кол-во немного не так я посчитал - было 5 переменных, добавили 2+6 в неравенства, и 3 переменных разбили на разность двух новых - итого переменных в канонической форме должно быть 5-3+2+6+2*3, так будет правильнее.

[Sega611]

Спасибо. Вроде все переписал
$Z=-c_1x_1-c_2x_2-c_3(x_3'-x_3'')-c_4(x_4'-x_4'')-c_5(x_5'-x_5'')\to min$
$a_1_1x_1+a_1_2x_2+a_1_3(x_3'-x_3'')+a_1_4(x_4'-x_4'')+a_1_5(x_5'-x_5'')+x_6=b_1$
$a_2_1x_1+a_2_2x_2+a_2_3(x_3'-x_3'')+a_2_4(x_4'-x_4'')+a_2_5(x_5'-x_5'')+x_7=b_2$
$a_3_1x_1+a_3_2x_2+a_3_3(x_3'-x_3'')+a_3_4(x_4'-x_4'')+a_3_5(x_5'-x_5'')-x_8=b_3$
$a_4_1x_1+a_4_2x_2+a_4_3(x_3'-x_3'')+a_4_4(x_4'-x_4'')+a_4_5(x_5'-x_5'')-x_9=b_4$
$a_5_1x_1+a_5_2x_2+a_5_3(x_3'-x_3'')+a_5_4(x_4'-x_4'')+a_5_5(x_5'-x_5'')-x_{10}=b_5$
$a_6_1x_1+a_6_2x_2+a_6_3(x_3'-x_3'')+a_6_4(x_4'-x_4'')+a_6_5(x_5'-x_5'')-x_{11}=b_6$
$a_7_1x_1+a_7_2x_2+a_7_3(x_3'-x_3'')+a_7_4(x_4'-x_4'')+a_7_5(x_5'-x_5'')-x_{12}=b_9$
$a_8_1x_1+a_8_2x_2+a_8_3(x_3'-x_3'')+a_8_4(x_4'-x_4'')+a_8_5(x_5'-x_5'')-x_{13}=b_8$
$a_9_1x_1+a_9_2x_2+a_9_3(x_3'-x_3'')+a_9_4(x_4'-x_4'')+a_9_5(x_5'-x_5'')=b_9$
$a_{10}_1x_1+a_{10}_2x_2+a_{10}_3(x_3'-x_3'')+a_{10}_4(x_4'-x_4'')+a_{10}_5(x_5'-x_5'')=b_{10}$
$x_1,x_2,x_3',x_3'',x_4',x_4'',x_5',x_5'',x_6,x_7,x_8,x_9,x_{10},x_{11},x_{12},x_{13}\geqslant 0$

Цитата:

У Вас ограничений типа "меньше либо равно" 2 шт., значит там должны появиться 2 переменные,
ограничений типа "больше либо равно" 6 шт., поэтому там должны появиться ещё 6 переменных.

Это я что-то вообще проморгал.

[Zealint]

Кажется правильно, пусть кто-нибудь еще проверит, чтобы надежней было.

Если бы я был Вашим преподавателем, то сделал бы замечание: когда индекс становится двузначным, то можно неправильно понять запить вида $a_{101}$, лучше написать $a_{10,1}$.