Скорее не путаю, а так думаю. Потому и спрашиваю у Someone, что надо считать размерностью, протяжённость предыдущей размерности или векторное к ней дополнение?
Существует много разных понятий размерности.
Самое простое - это алгебраическая размерность линейного пространства: количество векторов в его базисе. Пространство

, обычно определяемое как множество столбцов

действительных чисел с операциями покомпонентного сложения и покомпонентного умножения на действительные числа, имеет размерность

, потому что имеет базис из трёх векторов:

,

,

.
Одно и то же множество часто можно рассматривать как линейное пространство над разными полями. Например, множество действительных чисел

можно считать линейным пространством над ним самим (тогда оно одномерно), а можно - над полем рациональных чисел (тогда его размерность равна континууму). Другой пример - пространство
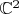
столбцов

комплексных чисел, которое двумерно над полем комплексных чисел и четырёхмерно над полем действительных чисел.
Для бесконечномерных пространств существуют разные определения базиса, поэтому возникают дополнительные варианты размерности (уже бесконечной).
В общей топологии существует множество различных определений размерности (затрудняюсь назвать их количество даже приблизительно). Основными являются лебегова размерность

, определяемая конечными покрытиями, и индуктивные размерности

и

, определяемые с помощью перегородок. Для метризуемого пространства

всегда

, причём, известен пример метриуемого пространства, для которого

, а

. Для более общих пространств, чем метризуемые, все три этих размерности могут оказаться разными. Вместе с тем,

и

. Кроме этих трёх, существует ещё множество других размерностей, определяемых как чисто топологически, так и через метрику или равномерные структуры. В алгебраической топологии есть свои определения размерности, не обязательно совпадающие с топологическими.
Все перечисленные размерности по определению являются целыми (индуктивные являются ординалами).
"Дробные размерности" фракталов в топологическом или алгебраическом смысле размерностями не являются. Очень простое объяснение этого феномена я нашёл здесь: "
Фрактальная размерность". Топологическая размерность обсуждаемой там звезды Коха равна

(уточнение: построение звезды Коха обычно начинают не с отрезка, а с равностороннего треугольника, поэтому то, что показано в рекомендуемой заметке - это треть звезды Коха). Из этого обсуждения можно также понять, что фрактальная размерность множества является не характеристикой этого множества самого по себе (звезда Коха с топологической точки зрения - это просто окружность, только "очень извилисто уложенная" на плоскость), а характеристикой расположения этого множества в

(или в

в более общем случае).