Найти неопределённый интеграл

[Mikle1990]

Проверьте пожалуйста.

\int \frac{dx}{x^3+x^2+x}= \int d(ln(x^3+x^2+x))= ln(x^3+x^2+x)+C

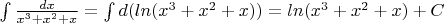
У меня очень много сомнений. Не могу понять, нужно ли раскладывать многочлен на множители и проводить дальнейшие операции.

Мне просто такой пример помогали решать (не на форуме)
\int \frac{dx}{x^3-5x^2+6x} =\int \frac{A*dx}{x} + \int \frac{B*dx}{x-2} + \int \frac{C*dx}{x-3} = ...

А может и первый пример надо тоже как-то так решать o_O

Помогите пожалуйста

[gris]

А делов то - продифференцировать результат и убедиться, что подынтегрального выражения никак не получается. Так что раскладывайте на простейшие дроби.

[Padawan]

(Оффтоп)

Меня прикалывают такие универсальные способы интегрировани

$$ \int f(x)\,dx =\int\frac{1}{f^{-1}(x)}\, dx=\int d\ln f^{-1}(x)=\ln f^{-1} (x)+C= -\ln f(x)+C $$

или по частям

$$ \int f(x)\, dx=xf(x)-\int x \,d\,f(x)=xf(x)-\int x f'(x)\, dx=xf(x)-\int f'(x)\, d\,\frac{x^2}{2}=xf(x)- f'(x)\frac{ x^2}{2}+C $$

[Mikle1990]

$\int \frac{dx}{x^3+x^2+x}= \int d(ln(x^3+x^2+x))= ln(x^3+x^2+x)+C$
это правильно?

Ведь можно и второй пример, который я дал, таким же способом. o_O
(но решается то он по-другому)

[gris]

Padawan пошутил. У джедаев трудно бывает детектировать иронию.

$(\ln (x^3+x^2+x))'=\dfrac {3x^2+2x+1}{x^3+x^2+x}$

Раскладывайте на простейшие дроби.
$\dfrac {1}{x^3+x^2+x}=\dfrac {1}{x(x^2+x+1)}=\dfrac {A}{x}+\dfrac {B+Cx}{x^2+x+1}$

[Mikle1990]

Спасибо. А как этот процесс называется?
"Нахождение интеграла путём интегрирования рациональной дроби с помощью разложения её на простейшие дроби" ?

[gris]

Зорич, Никольский "Интегрирование рациональных функций" через простейшие дроби.
Кудрявцев "Интегрирование рациональных дробей" через элементарные дроби
Фихтенгольц "Интегрирование рациональных выражений" через простые дроби.

В общем, сами придумайте название способа.

[Padawan]

Так и называется! Еще метод Остроградского выделения рациональной части есть.