есть две задачи, которые слегка ставят в тупик.
первая:
Пусть

и

- два топологических пространства,

- покрытие пространства X,
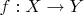
некое отображение. Ограничение

на произвольное

непрерывно. тогда доказать, что при выполнении любого из условий:
1) S открыто
2) S замкнуто и конечно
3) S замкнуто и локально конечно
отображение f будет непрерывно
вторая:
Пусть имеем многообразие

в

. нужно показать, что

будет касательным вектором к этому многообразию в точке E. Найти образ v под действием дифференциала отображения, которое ставит в сответствие матрице обратную к ней.
теперь о том, что именно ставит в тупик.
первая. По определению функция непрерывна на множестве, если непрерывна в каждой его точке. Таким образом, если она непрерывна на элементе покрытия, то и во всех точках этого элемента тоже. Поскольку покрытие - это покрытие, то функция непрерывна в каждой точке пространства и, значит, непрерывна на всем пространстве. так о чем, стало быть, задача?
вторая. При стандартном вложении

эта группа, очевидно, расположится на поверхности стандартной восьмимерной сферы радиуса 3. и очевидно, что эта матрица содержится в касательном пространстве к сфере в точке E, ибо она ортогональна нормали к сфере. Следует ли отсюда, что она будет лежать в касательном пространстве к многообразию? если посмореть на определение касательного пространства к поверхности и многообразию через векторы скорости всевозможных кривых, то кажется, что да. Так ли все просто?