Хотел бы обратить внимание не обсуждавшиеся еще вопросы доказуемости по данной проблеме. Возможно превеликое множество разных вариантов:
- не существуют полиномиальные

-полные алгоритмы (

);
-- существует доказательство несуществования полиномиальных

-полных алгоритмов, (

), степень неразрешимости

;
-- не существует доказательства несуществования полиномиальных

-полных алгоритмов, (

), степень неразрешимости
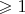
;
--- существует доказательство несуществования доказательства несуществования полиномиальных

-полных алгоритмов, (

), степень неразрешимости

;
--- не существует доказательства несуществования доказательства несуществования полиномиальных

-полных алгоритмов, (

), степень неразрешимости

;
и т.д......
- существуют полиномиальные

-полные алгоритмы (

);
-- ...(аналогичные вопросы разрешимости утверждения

решаются тривиально, см. ниже)...
Такие же цепочки вопросов можно поставить и в отношении свойств (полиномиальность,

-полнота) какого-либо конкретного алгоритма:
- данный алгоритм

обладает свойством

, (

);
-- существует доказательство того, что данный алгоритм

обладает свойством

, (

);
-- не существует доказательства того, что данный алгоритм

обладает свойством

, (

);
--- существует доказательство несуществования доказательства того, что данный алгоритм

обладает свойством

, (

);
и т.д......
- данный алгоритм

не обладает свойством

, (

);
-- ...(аналогичные вопросы разрешимости утверждения

)...;
здесь

- одно из свойств: полиномиальность,

-полнота.
Также, возможны различные утверждения относительно отдельных классов полиномиальных

-полных алгоритмов, обладающих одинаковой разрешимостью по этим свойствам:
- существуют указанные алгоритмы, для которых существует доказательства их полиномиальности и

-полноты (каждый из них можно найти явно);
- существуют указанные полиномиальные алгоритмы, для которых существует доказательство их

-полноты, но не существует доказательства их полиномиальности;
- существуют указанные алгоритмы, для которых существует доказательство их полиномиальности, но не существует доказательства их

-полноты;
- существуют указанные алгоритмы, для которых не существует ни доказательства их полиномиальности, ни доказательства их

-полноты;
...(прочие комбинации)...
полагаю, если некоторый класс не пусть, то и все классы с более неразрешимыми свойствами своих алгоритмов не пусты.
Можно рассмотреть аналогичные вопросы разрешимости, затрагивающие параметры полиномиальной сложности алгоритмов (

и

).
Есть ли какие либо результаты по перечисленным проблемам?
Простое доказательство существования полиномиальных

-полных алгоритмов не предполагает еще явного построения такого алгоритма, и поэтому оно, само по себе, полностью бесполезно для практической криптографии.
Если же у нас имеется конкретный полиномиальный

-полный алгоритм, то недоказуемость его полиномиальности и

-полноты в принципе не помешает его практическому использованию - за полиномиальное время мы всегда сможем получить и проверить результат.
Как же найти такой алгоритм, если он существует? На него можно выйти за конечное, заранее ограниченное, но возможно, никогда точно не известное, число шагов.
Простейший вариант: выберем какую-нибудь

-полную задачу и будем перебирать для нее все возможные алгоритмы по порядку (номер каждого алгоритма можно сделать б.-м. регулярно зависящим от длины его описания), на каждом шаге рассматривая для проверки только один алгоритм. Для первого шага рассмотрим первый алгоритм. Если рассматриваемый на

-ом шаге алгоритм для каждого из аргументов длины

от

до

дает правильное решение за время не более, скажем,

, то на следующем (

-ый) шаге будем рассматривать тот же алгоритм, иначе - на следующем шаге рассмотрим первый, еще не рассмотренный, алгоритм (следующий по порядку за алгоритмом

-ого шага). Рано или поздно, на каком-то шаге (его номер может быть очень велик) мы выйдем на какой-нибудь полиномиальный

-полный алгоритм, который далее не будет сменятся на всех следующих шагах (стационарный).
Если некоторый полиномиальный

-полный алгоритм имеет порядковый номер

и решает указанную задачу за время не более

при длине аргумента

, то он пройдет проверку для всех шагов

в данном случае, если и только если

. Мы выйдем на тот их полиномиальных

-полных алгоритмов, удовлетворяющих вышеуказанному условию, что имеет наименьший номер. Но мы никогда не сможем определить достигли ли мы этого алгоритма, если (что вполне возможно) для него невозможно доказать ни одной верхней оценки времени выполнения, вида

.
Такой (или подобный) алгоритм лучше использовать совместно с конкретными практическими вычислениями, по мере роста потребностей, находя алгоритм, применимый для все большего диапазона длин аргументов, но и со все большей допустимой временной сложностью.
Сам предложенный (перебирающий алгоритмы) алгоритм может быть использован как полиномиальный

-полный (когда

): если условием проверки рассматриваемого на

-ом шаге алгоритма будет получение алгоритмом правильного (проверяется) результата за время не более

, где

- длина аргумента. Данный

-полный алгоритм будет полиномиальным, в отличие от переборного (перебирающего результаты и проверяющего их) алгоритма.
Таким образом, существуют полиномиальные

-полные алгоритмы, то существует алгоритм с доказательством своей полиномиальности и

-полноты.
Предложенный алгоритм сам имеет номер, притом небольшой (посему, он, скорее всего, дойдет и до шага с собственным номером), а так как для того, чтобы дойти до стационарного полиномиального

-полного алгоритма, потребуется вероятно очень большое (но постоянное) число шагов, то предложенный алгоритм, рассматривая себя, скорее всего проверки не пройдет.