Алгебра и теория чисел задачи

[vox]

День добрый прошу помочь в решении
1.Сколько ожерелий можно составить из трех красных, шести синих и девяти белых бусин?
2.$G=(x,y|x^1^2=y^2=e,yxy=x^7) $. Доказать, что если $x^6 \ne e \ne x^4$, то |G| = 24 и G изоморфна группе $C_3 * D_4 , $ где $C_3$– циклическая группа, а $D_4$ – группа диэдра.

[Xaositect]

1. Теорема Пойа.

[ewert]

но вообще-то, между прочим, раз уж это ожерелья, то переворачивать их тоже можно.

[Xaositect]

ewert в сообщении #264373 писал(а):

но вообще-то, между прочим, раз уж это ожерелья, то переворачивать их тоже можно.

Ну и что? Теорема Пойа для любой группы формулируется.

[jetyb]

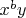
2) В условии не упомянуто, что в $G$ нет никаких других элементов $z$, ну это ладно. Можно показать, что элементы $\{x^a,x^ay\}_{a=0}^{11}$ попарно различны. Несложным упражненинем будет установление соответствия между $yx^a$ и $x^by$. Таким образом, полностью определится операция на группе, и установить изоморфизм будет делом техники.

[vox]

Xaositect в сообщении #264383 писал(а):

ewert в сообщении #264373 писал(а):

но вообще-то, между прочим, раз уж это ожерелья, то переворачивать их тоже можно.

Ну и что? Теорема Пойа для любой группы формулируется.

а разве не применяя лемму Бернсайда

[vox]

Да не густо с первой боле менее еще а вторая увы.