Задачи со II Всероссийской студенческой олимпиады по математике 2008 г. (предполагаю, что для студентов технических и экономических вузов):
1. (15 баллов, остальные задачи олимпиады оценивались не выше 12 баллов).
В трехмерном евклидовом пространстве даны

параллелепипедов с ребрами, параллельными координатным осям. Матрица

составлена таким образом, что на месте

стоит объем пересечения

-ого и

-ого параллелепипедов. Докажите, что

.
Собственно, здесь я пытался найти алгоритм приведения матрицы к треугольному виду, считая лишь, что

,

и

. Возможно, упустил какие-то условия из геометрической интерпретации, либо вообще нужно действовать по-другому.
2. (12 баллов)
Пусть

- единичный круг

. Точка

выбирается произвольным образом на границе круга

, а точка

- произвольным образом на внутренности круга

(эти точки выбираются независимо друг от друга и равномерно на своих областях определения). Пусть

- прямоугольник с диагональю
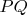
и сторонами, параллельными осям координат. Какова вероятность, что прямоугольник

целиком содержится в

?