Вот, "причесал" немного код:
Код:
Код:
#include <iostream>
typedef unsigned long ulong;
ulong Sum(ulong Number)
{
ulong Result=0;
do Result+=Number%10; while(Number/=10);
return Result;
}
int main()
{
ulong Year;
std::cin >> Year;
for(ulong Age=0; Age<Year; Age++)
if(Age==Sum(Year-Age))
std::cout << Year-Age << std::endl;
return 0;
}
Идею понял.
Да, я не программист по натуре и образованию

.
2_v_lЦитата:
оно тоже должно быть

-значным, это очевидно, но не доказывал
Это не так. Контрпример (первый попавшийся) для

:

. На деле,

(год рождения не может превосходить "текущий" год).
Моя вина, я имел в виду
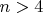
, для

проще не организовывать сложный алгоритм, а просто перебрать все варианты. Как оказалось, я вообще не в том направлении двигался.
Вы доказывали, что для любого целого

решение (

), вообще говоря, не единственно (а для некоторых

решений не существует)?
Нет, но процессе работы над первой версией программы обнаружил, что возможны два решения. Кстати, если посмотреть на мой алгоритм (нет, просто рассуждения), то возможны двойные решения. Возможны, но опять-таки не проверял, тройные и большее количество решений. Меня заинтересовала длина цепочки, см. мой первый пост.
P.S.: Интересно, можно ли вывести прямую формулу, без цикла?
Если честно, то не понял суть вопроса. Если вы имеете в виду конечную алгебраическую/арифметическую формулу, то незнаю, получится ли, т.к. возможны более чем два решения.
P.S. На разработку такого странного алгоритма меня натолкнуло не только то, что я не программист, но и то, что при больших

, количество циклов остаётся ограниченным (я не прав?), или, скорее всего так, количество бесполезных циклов уменьшается.
Приведённый код работает отлично для малых чисел (1998, 9999, 10001). Но я попробовал его при 12345678910, сразу появилось решение 12345678860 и долгая пауза. Очевидно, что других решений не будет (если

имеет другую кратность чем

, о чём говорил выше, но не выделил особо) и цикл будет работать в пустую.
А теперь вспомним, что unsigned long это до

, а unsigned long long это до

. Так что в холостую тратить ресурсы нас научили
