Вывести рекуррентное соотношение.

[Alex696]

Здравствуйте. Есть несколько вопросов касательно рекуррентных соотношений.
Заранее благодарен за ответ.

1. Если есть некая сумма чисел с переменной от $i --> n$ (индекс члена последовательности), рекуррентным соотношением будет называться:

а). формула, где произвольный член суммы будет находиться за неким преображением на основе первого члена последовательности.

б). формула, где произвольный член суммы будет находиться за неким преображением на основе первого или любого другого известного члена последовательности.

в). может задаваться любой формулой, лижбы соблюдалась закономерность между членами данной суммы.

Допустим дана сумма $sin(k*x) + ... + sin(n*x)$, где $k=1, k --> n$. Что будет рекуррентным соотношением, выражающим произвольный член суммы $a(n)$? На что обращать внимание?

[Sonic86]

Alex696 писал(а):

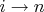
1. Если есть некая сумма чисел с переменной от $i \to n$ (индекс члена последовательности), рекуррентным соотношением будет называться:

а). формула, где произвольный член суммы будет находиться за неким преображением на основе первого члена последовательности.

б). формула, где произвольный член суммы будет находиться за неким преображением на основе первого или любого другого известного члена последовательности.

в). может задаваться любой формулой, лижбы соблюдалась закономерность между членами данной суммы.

Это Вам такое определение рекуррентного соотношения дали? Я, честно говоря, таких определений не видел, но что-то тут не то, нечетко сформулировано или что-то опущено.
Можно так: если $f(n)$ - некоторая функция (ну или последовательность ее значений), рекуррентным соотношением для нее называется формула вида $g(f(n-1),f(n-2),...,f(n-k))=0$ с начальными условиями $f(1)=f_1,f(2)=f_2,...,f(k)=f_k$. Например, $f(n)=f(n-1)+f(n-2),f_1=f_2=1$ - рекуррентная формула для чисел Фибоначчи. Хотя явно не все рекуррентные формулы имеют такой вид, например, формула $f(n)=f(n-1)+...+f(1), f(1)=1$. Ну да ладно.

Alex696 писал(а):

Допустим дана сумма $sin(kx)+...+sin(nx)$, где $k=1, k \to n$. Что будет рекуррентным соотношением, выражающим произвольный член суммы $a(n)$? На что обращать внимание?

.
А вот тут я Вас не понял. Видимо $k = const$. А что такое $k \to n$? Ведь $k$ - натуральное число, устремлять его никуда нельзя.
Только если так: дано:
$S(n)=sin(kx)+...+sin(nx)$ - формула суммы
$a(n)=sin(nx)$ - формула $n$-о члена, $a(k)=sin(kx)$ - начальное условие. Надо написать рекуррентное соотношение для $S(n)$ с помощью $a(n)$. Это просто. Рассмотрите $S(n)-S(n-1)$.

[Алексей К.]

Я только поправлю Ваше словоупотребление. Чем заменить "преображение" --- найдите сами.

Alex696 в сообщении #253177 писал(а):

Допустим дана сумма $sin(k*x) + ... + sin(n*x)$, где $k=1, k --> n$.

Один вариант записи этой фразы: "... дана сумма $\sin x +\sin 2x + ... + \sin nx$". И никаких $k$, сбивающих с толку.
Второй вариант: "... дана сумма $\displaystyle\sum\limits_{k=1}^{n} \sin kx$".
А вот при смешивании двух стилей получается несуразица.

Alex696 в сообщении #253177 писал(а):

Что будет рекуррентным соотношением, выражающим произвольный член суммы $a(n)$?

А что такое член суммы??? Вполне рекуррентно: $a(1,x)=\sin x,\quad a(n,x)=a(n-1,x)+\sin nx$.

Alex696 в сообщении #253177 писал(а):

На что обращать внимание?

В частности, на словоупотребление. И, признаться, не очень понятно, что Вам не понятно.
Определения из учебника?

[Alex696]

2Sonic86: Спасибо за пояснения! Я так понял $S(n) = S(n-1) + a(n), где a(n) = sin(nx)$

Еще один пример: Допустим есть

$(cos1/sin1) * (cos1 + cos2/sin1 + sin2) *...* (cos1+...+cos n/sin1+...+sin n) $

Рекуррентным соотношением будет

$S(n) = S(n-1) * a(n), где a(n) = (cos1+...+cos n/sin1+...+sin n)$.

[Sonic86]

Alex696 писал(а):

Я так понял $S(n)=S(n-1)+a(n)$, где $a(n)= \sin(nx)$

Ага!

Alex696 писал(а):

Еще один пример: Допустим есть
$(\cos 1/ \sin 1) \cdot (\cos1+ \cos2/ \sin1 + \sin2) \cdot (\cos1+ \cos n/ \sin1 + ... + \sin n)$
Рекуррентным соотношением будет
$S(n)=S(n-1) \cdot a(n)$, где $a(n) = \cos 1 + ... + \cos n/ \sin 1 + ... + \sin n$.

Да, все верно. Хотя мне немного непонятна формула для $a(n)$, но ответ правильный
Кстати, наведите мышкой на формулы - в качестве подсказки вылазит тэг, которым эти формулы пишут.