Проверьте пожалуйста правильность решения.
Дано уравнение

.
Является ли решение единственным.
Рассмотрим

где

два решения системы.
Тогда


Найдём первоначальные условия
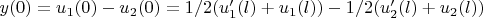

Следовательно,

.

так как

.
Следовательно,

.
Теперь

,

.

.
Таким образом, если решения

совпадают в точке 0

, то решения совпадают для всех

.
То есть решение единственно.