энтропия

[nokal]

Здравствуйте, Господа

Вот с такой проблемой для себя столкнулся, читая учебник по термодинамике. Я так понял что данный форум лучше всего подходит для вопросы по термодинамике.

Изучая второе начало, познакомился с понятием энтропии, изменение которой определяется как:
$dS = \frac Q T$
и определена она для изотермического процесса.

Вот только я не могу понять, как это может передаваться теплота при изотермическом процессе, когда оба тела имеют одинаковую температуру. Ведь само Q по определению это энергия выраженная в изменении температуры. А тут говорят что процесс изотермический

[PapaKarlo]

Речь идет о квазистатическом процессе. Упрощенно такой процесс вроде бы и описывает какое-то изменение, но очень мелкими шажками, а в промежутках ничего не меняется. Т.е. процесс "кусочно-изотермический". Естественно, это идеализация, представление очень медленного процесса, при котором тепло передается очень маленькими порциями. Изменение энтропии определяется как $dS=\frac{\delta Q}{T}$

[Парджеттер]

Парджеттер:

Не вижу ничего дискуссионного. Перенесено в "Помогите решить/разобраться (Ф)".

[Comanchero]

nokal, Вам должно быть известно что при плавлении тв. тела, а также при кипении жидкости-температура не меняется, однако требуется постоянный подвод теплоты. Вот это изменение в системе как раз и заложено в увеличении энтропии. И вообще все самопроизвольные процессы, происходящие в природе направлены на не уменьшение энтропии (Второе начало термодинамики).

[Romio]

nokal в сообщении #232941 писал(а):

Вот только я не могу понять, как это может передаваться теплота при изотермическом процессе, когда оба тела имеют одинаковую температуру. Ведь само Q по определению это энергия выраженная в изменении температуры. А тут говорят что процесс изотермический

Вы тут уже ошибаетесь, пример с плавлением очень хорошо это объясняет. Путаете процессы (вообще говоря, изотермический и адиабатический), теплота при изотермическом процессе, конечно, может изменяться, а температура остается постоянной, а вот при адиабатическом процессе, когда отсутствует теплообмен, то теплота не изменяется.

[Хет Зиф]

PapaKarlo
Не очень понятно, что значит кусочно - изотеремический?

Главное в квазистационарных процессах их обратимость. Но замечательность энтропии состоит в том, что это есть функция состояния, и не зависит от того как система переходила из одного состояния в другое. Квазистационарные процессы -удобный способ вычислить энтропию (с точностью до константы). Не в квазистационарных процессах равенство

$$dS = \frac{dQ}{T}$$

не выполненно. А выполненно неравенство, и там можно приговаривать второй закон термодинамики и.т.д.

[Romio]

Хет Зиф

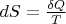
Вы немножко неправильно написали равенство теплота с мат. точки зрения не является полным дифференциалом, поэтому знак дифференциала нельзя употреблять, нужно иметь ввиду что , где есть различия в обозначении малых величин, т.к. Q функция процесса, а не состояния.

-- Пт авг 21, 2009 12:26:08 --

Как я понял под "кусочно-изотермическим" имеется ввиду процесс, отдельные малые части которого можно приближенно считать изотермическими.

И, кстати, автору темы очень полезно почитать о статистическом смысле энтропии, должно все сразу стать понятно, у Матвеева, по-моему, очень хорошо написано.

[Хет Зиф]

Romio

Я согласен. Но можете ли вы привести пример где такая неточность приведет к ошибке: например вы приводите задачу, и показываете, что если записать

$$dS = \frac{dQ}{T}$$

, то мы решим ее неправильно.

Это как то не верно, отдельные части считать изотермическими. Вы же когда рисуете гипотенузу прямоугольного треугольника не считаете отдельныее ее части параллельными катетам.

[Romio]

Я написал, что возможно это имелось ввиду, как то по другому понять это выражение у меня не получается. Можем же мы считать в анализе функцию кусочно- гладкой Но здесь это действительно ни к чему.

Вот и имеется ввиду различный математический смысл. В полном дифференциале результат не зависит от порядка слагаемых, а если будем считать δQ то получим разные результаты если сначала будем менять порядок слагаемых. Конечно, величины очень похожи.

[Хет Зиф]

Romio
Если Вам не трудно, то уточните пожалуйста еще раз, что Вы понимаете под

$$ dQ$$

и под

$$ \delta Q$$

[Romio]

Дифференциал функции и малое приращение соответственно.

Полный дифференциал может характеризовать функцию состояния, но Q не является функцией состояния, зависит от конкретного процесса и пути по которому происходит процесс, и как полный дифференциал быть записана не может.

[Хет Зиф]

Как-то не осознаю физической разницы, вот в 5 томе Л.Л. вроде написано

$$dQ$$

.
Все таки объясните мне, к каким недоразумениям это может привести.

[Romio]

На простом примере возьмем круговой процесс, пусть он идет из точки 1 в т. 2 и затем обратно. Круговой $\int dQ=0$(формально), а $\int \delta Q\not =0$.

Вообще строгое доказательтсво почему в случае двух и более переменных, а вообще говоря и 1 ( но для функции 1 переменной можно практически всегда рассматривать б.м величину, как бесконечно малое приращение некоторой функции) не всегда удается указать б.м приращение функции, указывающее в явном виде величину, о приращении которой идет речь, можно найти в книге Матвеев "Молекулярная физика" 1981г. стр. 125

[Хет Зиф]

Romio
Спасибо! Прочитал, стало более понятно. Правда я никогда не сталкивался со сложностями при данных обозначениях. Наверно это больше для понимания

[barga44]

Вот только я не могу понять, как это может передаваться теплота при изотермическом процессе,

А вы всегда ставьте опыт.Возьмите кипящую воду в кастрюльке и подведите тепло, так что вся вода испарилась.Температура кипящей воды 100С.
Отсюда понятно что этот процесс необратим, значит оператор диффенциала не справедлив для энтропии.
Так и изучали физику 100 лет назад.Без философии.