1) Из условия

, тогда

.
Предположим противное, тогда

, тогда аналогичную цепочку сравнимостей можно начать с любого элемента

, например, с

. Но тогда

, а так как

, то

- противоречие с условием.
-- Чт июл 23, 2009 00:13:54 --5)

, если я ничего не напутал.
Положим

, получим тройку

, которая является множеством длин сторон некоторого треугольника. Из неравенства треугольника получаем

. Если

, то положим

, тогда

, то есть

является

-периодичной. Положим

, получим тройку

, в которой

- противоречие. Значит,

.
Положим

, получим тройку

, откуда

. Значит, все

разбивается на две части: числа

, для которых

, и пары чисел

, где
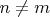
, таких что

.
Предположим, что

не является тождественной, тогда вторая часть непуста. Выберем наименьшее число

, участвующее в парах второй части, положим

. Если

, то положим

- числа из первой части, для которых

; получаем тройку

, в которой

- противоречие.

не может быть единицей, так как

, значит,

; По-прежнему

. Положим

, получим тройку

, откуда

.

- биекция,

, поэтому

, откуда

. Теперь положим

, получим тройку

. Аналогично получаем, что

. Продолжая далее, имеем

и наоборот:

для

. Положим

, получим

, так как

. Противоречие с тем, что

.
Значит, вторая часть пуста, первая часть совпадает с

, откуда

.