Определение площади даёт лемма 2.
смотрю и не вижу. Приведите определение площади для 'гладкой' в Вашем определении поверхности...Уже много набралось Ваших 'можно доказать'.
пока что по части 'доказать' у Вас слабовато получается...Да, еще, почитайте
Правила форумаВы задаётё так много вопросов, что я просто не успеваю на них отвечать. Задавать то вопросы легче. В то время как каждый ответ требует времени. Я просил ранее Вас задавать их по одному.
Отвечаю на один из последних. По моему определению поверхность глакая, если к ней в каждой точке можно провести касательную плоскость. Для каждого
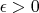
находим на поверхности достатчно большое число точек, касательные плоскости которых содержат куски площади и диаметра меньше чем
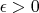
, причём так, что эти куски составляют некоторую ломанную поверхность. В пределе, когда

сумма площадей этих кусков стремится к площади поверхности. Это общее определение, но именно его я и придерживаюсь.
Если поверхность A гладкая и если выполнены условия леммы 1, и если точка

поверхности A, площадь которой мы считаем, стремится к точке

, расположенной так же на поверхности, то касательная плоскость в точке

стремится к касательной плоскости в точке

. Поскольку, касательная плоскость точки

может быть сколь угодно точно приближена касательными полоскостями поверхностей, стремящихся к A (это ещё надо доказать в лемме 1). Из-за этого (при условии, что доказана гладкость предельной поверхности), верна лемма 2.
Однако, это ещё не тот ответ, котрый я хочу вам дать.