Если расстояние между точками уменьшается, то после операций
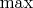
и
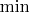
оно должно также уменьшатся.
мне нужно показать, что

, а слева и справа от неравенства
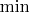
и
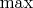
берутся по разным множествам, так что вроде не факт.
-- Пт июл 10, 2009 22:21:29 --Хотя да, можно перейти к одинаковым максимумам и минимумам:


.
Также понятно, что можно ограничиться только линейными преобразованиями
так как

.
А что дальше непонятно

. Стандартное же начало, что предположим, что внешний максимум достигается на первом аргументе, ничего не даёт увидеть.