Вроде совсем легко.
Пусть

--- не сюрьекция. Тогда одно из действительных чисел не попадает в область значений

. Без ограничения общности можно считать, что это число

.
В силу непрерывности имеем

либо

для всех

. Опять же без ограничения общности будем считать, что выполнено первое.
Прообраз ограниченного множества
![$[0,f(0)]$ $[0,f(0)]$](https://dxdy-02.korotkov.co.uk/f/5/0/3/503f5a2e771cbef01a357a9a16fc736382.png)
ограничен. Значит, существует

, такое что

.
Далее. Так как

непрерывна, то на компакте
![$[-M,M]$ $[-M,M]$](https://dxdy-04.korotkov.co.uk/f/3/8/9/38918d96e6d96577491757099030d9d482.png)
она достигает минимума. Ясно, что это будет глобальный минимум функции

. Опять же без ограничения общности можно считать, что этот минимум достигается в нуле.
Выберем открытое

, такое

и

гомеоморфны и гомеоморфизмом является функция

(в ограничении на

).
Так как областью значения указанного гомоморфизма является всё

, то

.
Выберем
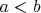
, такие что

. Это можно сделать в силу открытости

. Кроме того, имеем

.
Ограничение гомеоморфизма

на подмножество

есть опять же гомеоморфизм. Значит, можно считать, что

и

является связным множеством. Осталось показать, что

не связно и получить противоречие c тем, что

и

гомеоморфны.
Прообраз ограниченного множества
![$[0,b]$ $[0,b]$](https://dxdy-03.korotkov.co.uk/f/e/f/6/ef62f76cd147a280018fe9ac25fba7b282.png)
ограничен. Следовательно, существуют

и

, такие что

и

. Но непрерывная функция

обязана принимать на отрезке
![$[x_0,0]$ $[x_0,0]$](https://dxdy-04.korotkov.co.uk/f/7/0/b/70b47e0fc29b39bb8acf765445c4ab6b82.png)
все значения между

и

; аналогично,

принимает все значения между

и

на отрезке
![$[0,x_1]$ $[0,x_1]$](https://dxdy-04.korotkov.co.uk/f/7/a/9/7a9c388f2d92ca25f807de0f3a6bae2382.png)
. Значит,

и

для некоторых

и

. Таким образом,

содержит отрицательное число

, положительное число

и не содержит

.
Вот и всё

P. S. В названии темы допущена грамматическая ошибка.