Задача на нах. мн. цел. реш. ур. в R2

[Somewhere far beyond]

Пусть задано число $n\in \mathbb{N}$.
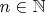
Будем говорить, что число $N \in \mathbb{U}^n$, тогда и только тогда, если $N*2^n \in \mathbb{Z}$. Из определения, $\mathbb{Z}\subset \mathbb{U}^n\subset \mathbb{Q}$ $\forall n\in \mathbb{N}$.
Пусть на компакте $x\in[t,t^2]$ задано уравнение вида $y=ax+b$, где $a,b\in \mathbb{U}^n$, t>1, t \in \mathbb{R}.
Требуется найти множество всех близко целочисленных решений уравнения алгоритмом в котором количество операций не превосходит некий полином $P(n)$.
Близко целочисленным решением будем считать, такую пару чисел $(x,y)\in \mathbb{Z}^2$, если существует уравнение $y=a_\alpha x+b_\beta$, где $a_\alpha \in[a-\alpha,a+\alpha], b_\beta \in[b-\beta,b+\beta]$, где $\alpha<<a,\beta<<b$, \alpha \in \mathbb{R}, \beta \in \mathbb{R}, для которого пара чисел является решением.
$a,b,\alpha,\beta,t заданы.

Заранее спасибо!