Помогите разобраться: есть несколько процессов, аналогичных по своей физической природе, зависимость одной величины
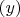
от другой

в каждом случае описывается уравнением типа:

, где

и

- некоторые постоянные величины (принимают различные значения для каждого из процессов). Требуется определить количество нетривиальных критериев подобия этих физических процессов.
(Мое решение):
Согласно ПИ-теореме, число нетривиальных критериев подобия
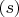
равно разнице между числом различных размерностей величин

, входящих в это уравнение, и числом независимых размерностей

:

.
Рассмотрим два примера.
1. Пусть
![$[y] = [b] = \text{см}^2$ $[y] = [b] = \text{см}^2$](https://dxdy-04.korotkov.co.uk/f/f/b/f/fbfa9b76887c6e1c3ed86f4cfbbced2482.png)
,
![$[a] = [x] =\text{см}$ $[a] = [x] =\text{см}$](https://dxdy-04.korotkov.co.uk/f/3/4/c/34c136394eafdc2a33afc33f0d0ec9d182.png)
,
в этом случае

,

, и соответственно

Нетривиальным критерием подобия, в этом случае является величина

, где

- некоторый характерный размер.
2. Пусть
![$[y] = [b] = \text{см}^3$ $[y] = [b] = \text{см}^3$](https://dxdy-03.korotkov.co.uk/f/a/0/f/a0fd4e0ddab6f13a1e6c2a9c3f51f14e82.png)
,
![$[a] = \text{см}^2$ $[a] = \text{см}^2$](https://dxdy-04.korotkov.co.uk/f/f/d/c/fdc9bed835e453bc7d9cbfd706c3abc382.png)
,
![$[x] =\text{см}$ $[x] =\text{см}$](https://dxdy-04.korotkov.co.uk/f/b/6/6/b66b59b2a8330bdc061623170b4031b282.png)
,
в этом случае

,

, и соответственно

Нетривиальными критериями подобия, в этом случае являются величины:

и

, где

- некоторый характерный размер.
Такое решения правильное, или я что-то непонимаю????????????????