О, только не раскладывайте её как функцию общего вида! Впрочем, Вы всего лишь проделаете лишнюю работу по вычислению коэффициентов, которые заведомо равны нулю. Именно для избежания лишней работы перед раскладыванием в ряд Фурье и определяют вид функции.
Ступенчатая функция состоит из кусочков постоянных функций, но сама константой не является. Так же и с чётностью. Но и тут Вы ошибаетесь. Определённая на интервале
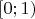
функция

не является ни чётной, ни нечётной.
Но вернёмся к аналитическому определению вида Вашей функции. Итак,
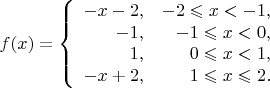
Теперь рассмотрим
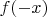
.
Пусть
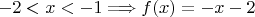
Но если
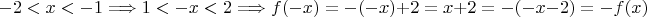
.
Аналогично
Пусть

Но если
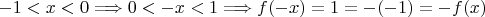
.
Пусть

Но если
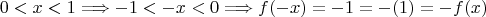
.
Пусть
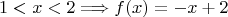
Но если
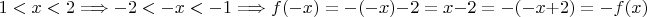
.
Итак,
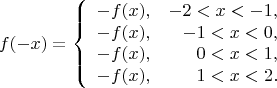
В отдельных точках
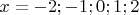
можно не проверять вид функции.
Вот достаточно строгое доказательство
невинности нечётности

именно для разложения в ряд Фурье, то есть за исключением одной точки.