Дана 5 мерная ассоциативная алгебра А (матрица 4 на 4)....
Ничего не понимаю. Множество этих матриц замкнуто относительно сложения и умножения, так что это действительно подалгебра в алгебре всех матриц четвёртого порядка. Эта алгебра 5-мерна и в качестве одного из возможных базисов напрашивается следующий:

Здесь

- единичная матрица,
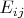
- матричная единичка, то есть матрица с единственной единичкой на пересечении

ой строки и

го столбца. У Вас это

.
Четырёхмерных подалгебр без единицы в ней много, но одна из них напрашивается сразу - это подалгебра, порождённая последними 4-мя элементами указанного базиса. Это просто подалгебра матриц указанного Вами вида только с

. Матрицы

в ней нет - это ясно, но и никакая другая матрица не будет нейтральным элементом при умножении на остальные.
Может быть об этом Вы хотели сказать ниже?
Цитата:
я хочу из этой 5 мерной ассоциативной алгеброй с единицей получить 4 мерную алгебру (без единицы, удаляя единицу).
А вот здесь вообще не разберу, о чём это:
Цитата:
Вопрос! В качестве базисных элементов я беру 1 (единицу)

,

а как подобрать пятый базис?