Всё правильно. Для непосвящённых количество обратимых матриц взаимно простых с простым

вычисляется как набор из

векторов. Первый можно взять любой кроме 0 (всего

), каждому выбору первого вектора соответствует

возможных выборов второго вектора (не принадлежащих одномерному подпространву порождённым первым вектором) и т.д., что даёт всего

Вообще то Арнольд интересуется и структурой этой группы, в частности тем, чему равен максимальный порядок циклической группы
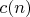
, образованной такой матрицы. Из того, что имеется мультипликативность значение
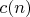
как и для чисел будет вычисляться как НОК по примарным разложениям. Однако, примарные разложения не являются циклическими группами как для чисел и поэтому вычисление
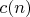
не такое простое для степеней простых чисел. Тем не менее оно вычисляется и предлагаю это сделать другим.