// Отредактирован заголовок. Первоначальный: "Теория вероятности". / GAA
_________________________________________________________________
Прибор состоит из 3-х элементов 1-го типа и 2-ух элементов 2-го типа.,
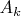
(к=1,2,3)-исправен к-ый блок;

(j=1,2) - исправен j-ый блок 2-го типа; C- прибор исправен. Прибор исправен в том случае, когда исправны не менее 2-х элементов 1-го типа и хотя бы один элемент 2-го типа. Записать С через
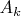
,

Ответ: C=2
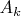
*

Правильно?