Здесь действительно всё вертится вокруг теоремы Банаха-Штейнгауза, но всё же не напрямую. Отталкиваемся от теоремы о замкнутом графике:
"Линейное отображение из банахова пространства  в банахово пространство
в банахово пространство  , определённое на всём
, определённое на всём  , ограничено тогда и только тогда, когда его график замкнут."
, ограничено тогда и только тогда, когда его график замкнут."
Здесь под графиком отображения

понимается линейное подмножество

декартового произведения

; последнее представляет собой банахово пространство относительно естественной нормы

.
Так вот. Пусть

. Пусть

-- "проектор" на

в том смысле, что каждому
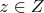
он ставит в соответствие единственный

из разложения

. Если все три подпространства

,

и

замкнуты, то и график этого оператора тоже замкнут. Действительно, из

следует

и

, но тогда и

. Это означает, что

, где

и

, т.е. предельная точка

.
Следовательно, по теореме о замкнутом графике оператор

ограничен, а ровно это и требовалось доказать.
(Ну можно ещё сослаться не на теорему о замкнутом графике, а, скажем, на теорему о непрерывности обратного; а вот как так сходу и непосредственно на Банаха-Штейнгауза -- не знаю.)