тогда искомой функцией будет

.
Вот на самом деле нехорошо, так как такая функция может быть плохой в точках

(вплоть до разрывности). Нужно омеги еще на какие-нибудь коэффициенты домножить, быстро стремящиеся к нулю. Ну то есть последить за высотами
![$h_n=\max\limits_{[a_n,b_n]}|\omega_{a_n,b_n}|$ $h_n=\max\limits_{[a_n,b_n]}|\omega_{a_n,b_n}|$](https://dxdy-04.korotkov.co.uk/f/b/3/b/b3b535e4be1848552aef2d48dcea2be082.png)
.
Добавлено спустя 7 минут 40 секунд:
А вообще, знаете ли, я чего-то засомневался, что решение есть вообще.
Несложно показать, что в любой неизолированной точке

последовательность производных

будет неограничена. Не знаю, правда, что отсюда следует ...
Добавлено спустя 2 минуты 45 секунд:
Можно пытаться по индукции омеги строить.
А слабо для
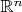
?
 Добавлено спустя 6 минут 13 секунд:
Добавлено спустя 6 минут 13 секунд:
Таак, припоминаю, что получил эту задачу на экзамене по дифференциальной геометрии и не решил. Экзамен принимал
он. Несмотря на всё это, я получил пятерку. Насколько я помню, экзаменатор не продемонстрировал явно знания решения этой задачи, хотя выдвинул гипотезу а-ля
мат-ламер, что функция от расстояния должна прокатить (или даже квадрат расстояния что-ли). Но потом дал другую задачку, ближе к теме, и я ее решил.

А эту, как видите, до сих пор не знаю ...
 Добавлено спустя 3 минуты 10 секунд:
Добавлено спустя 3 минуты 10 секунд:
Не, с функцией от расстояния плохо дело. Ясно, что общей такой функции даже для всех множеств вида

быть не может.