Brukvalub писал(а):
Вычислим расстояние между отрезками I=
![\[[0\;;\;1]\] \[[0\;;\;1]\]](https://dxdy-02.korotkov.co.uk/f/5/8/5/5854644fc3fe5fe368317952735747cf82.png)
и J=
![\[[0,5\;;\;3]\] \[[0,5\;;\;3]\]](https://dxdy-04.korotkov.co.uk/f/f/8/2/f8255ed1a4b160d6a0f5f40e4c307bb682.png)
.
....
Поэтому
![\[
d(I\;;\;J) = 2.5
\] \[
d(I\;;\;J) = 2.5
\]](https://dxdy-04.korotkov.co.uk/f/b/f/2/bf24b3ca4d433b62eb822694fd2d622d82.png)
Да, молодец, моего образования на это тоже хватило. Только я рассматривал не нахлестнутые отрезки, а скрещивающиеся отрезки на плоскости. Проблема тут в другом. Для двух соседних триангуляций

и

формулы получатся очень корявые (думаю я). Вряд ли задача имеет прямое аналитическое решение через вычисление этих расстояний. Например, я
не могу себе представить две триангуляции, расстояние между которыми было бы меньше
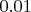
- а они есть!...