Доказать, что уравнение имеет единственный корень

[Colte]

Хочется понять как доказывать,что в ур-е
$3^{3 x -x^2-1}-3^{x^3-1}=2$
имеет всего один корень $x=1$ ?

Посмотреть на производные - нам жизнь не упрощает,
Решив $x^3-1>3 x -x^2-1$ получил,что корни могут лежать только в $(0 ; 1.31)$ ,где $1.31$ -приближенное значение.

[gris]

Попробуйте найти экстремумы левой части уравнения

[Андрей123]

Colte писал(а):

Хочется понять как доказывать,что в ур-е
$3^{3 x -x^2-1}-3^{x^3-1}=2$
имеет всего один корень $x=1$ ?

Посмотреть на производные - нам жизнь не упрощает,
Решив $x^3-1>3 x -x^2-1$ получил,что корни могут лежать только в $(0 ; 1.31)$ ,где $1.31$ -приближенное значение.

А при $x<\frac{3}{2}$ функция $3 x -x^2-1$, а вместе с ней и функция $3^{3 x -x^2-1}$ убывают. Функция $-3^{x^3-1}$ убывает везде. Сумма двух убывающих - убывающая.

[gris]

Вот уж нет. $3x-x ^2-1$ как раз возрастает на указанном интервале.

[Colte]

Насчет экстремумов:
$3^{3 x -x^2-x^3-1}(3-2x)-1=0 \ <=> \ f '(x)=0 $
Видно,что $x=1$ -решение $f '(x)=0$

P.S.Производная исправлена.

[gris]

И что это за экстремум? Уж не максимум ли? И каково же экстремальное значение функции?
А как это Вы производную посчитали?

[Colte]

Это должен быть максимум.Только как понять,что ещё нулей производной нету?

[gris]

$y=3^{3 x -x^2-1}-3^{x^3-1}$

$y'=\ln 3 (3-2x) 3^{3 x -x^2-1}-\ln 3\cdot x^2 3\cdot 3^{x^3-1}=0$

$(3-2x)\cdot 3^{3 x -x^2-x^3-1}- x^2 =0$

[ewert]

да, занудная какая-то задачка.

Имеем: $f(x)=g(x)$, где $f(x)=3^{3x-x^2}$ и $g(x)=3^{x^3}+6$;

с точностью до несущественного общего множителя $\ln 3$:
$f'(x)=(3-2x)3^{3x-x^2}, \qquad g'(x)=3x^23^{x^3};$
$f''(x)=\big(-2+(3-2x)^2\ln3\big)\cdot3^{3x-x^2}, \qquad g''(x)=\big(6x+9x^4\ln3\big)\cdot3^{x^3}.$

В точке $x_0=1$ наблюдается касание левого и правого графиков, т.к. там $f(x_0)=g(x_0)$ и $f'(x_0)=g'(x_0)$.

При этом $f''(x_0)<0$ и $g''(x_0)>0$, т.е. в окрестности точки касания (до тех пор, пока $f(x)$ остаётся выпуклой вверх и $g(x)$ выпуклой вниз) график левой части лежит ниже графика правой.

Корни второй производной левой части:

$$x_{1,2}={3\over2}\pm\sqrt{1\over2\ln3}\approx1.5\pm0.67$$

.

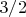
Вплоть до точки $3/2$ соотношение выпуклостей сохраняется, а дальше левая часть начинает убывать и с правой не пересечётся.

На отрезке от нуля до точки $x_1\approx0.83$ (пардон, в уме, но запас точности там вроде есть) пересечение тоже невозможно, т.к. обе функции растут и при этом $g(0)=9>f(x_1)\approx3^{1.8}$.

Наконец, тем более не может быть пересечения левее нуля: там $f(x)<1$ и $g(x)>6$.

Так что никакие общие точки, кроме единицы, невозможны.

----------------------------------------------------
И каких-то существенных упрощений тоже чего-то не видать...