Спасибо большое, уважаемые друзья
Someone,
Schwungrad.
Может быть получится раздобыть Matlab. Но я не учусь на мех-мате.
У меня, к Вам,
Schwungrad, возник вопрос по Matlab/Simulink + SimMechanics. Можно ли там самому создавать двухмерные детали желаемой формы, рельефа и задавать коэффициенты трения? Или там стандартный набор заранее предусмотренных механических деталей? Например, можно ли там смоделировать заводной механизм часов, состоящий из храповика и пружины? Или моделирование храповика там не предусмотрено?
Или можно смоделировать рельсу с зубчиками направленными в одну сторону, а поверх брусок с зубчиками в другую сторону?
Код:
____________
|____________|
/ / / / / / /
/ / / / / / / / / / / / /
-------------------------
Если этот брусок толкать вправо, то он скользит, а если влево, то сцепляется зубчиками и не скользит.
Например, сложное тело, описанное массивом частиц летит и вращается относительно некоторой инерциальной системы координат ИСО1 без соударения с другими телами. У центра масс тела вектор скорости

постоянный.
Рассмотрим инерциальную систему отсчёта ИСО2 с тем же масштабом, что и у ИСО1, начало координат которой совпадает с центром масс тела. Скорость центра масс в ИСО2 равна 0. Вектор скорости каждой частицы

.
Получается, что в ИСО1 вектор скорости каждой частицы

.
Для твёрдого тела можно хранить координаты центра масс

, суммарный импульс
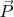
относительно ИСО1, суммарный момент импульса

относительно ИСО2 и кватернион

ориентации тела в пространстве. И хранить координаты частиц тела относительно ИСО2 без поворотов. А при расчётах, и отображении средствами OpenGL, умножать на матрицу поворота и сдвигать на нужный вектор.
Определить на C++ функцию
void Update(FLOAT dt)
{
...
}
dt - прирощение времени относительно предыдущего вызова Update. Например, если Update срабатывает каждые 0.001 секунд, то dt = 0.001. При реальной работе на компьютере dt не будет константой и будет тем меньше, чем мощнее компьютер.
Тогда задача ставится, найти новые значения

, зная предыдущие значения

и величину dt.
Для сложных тел можно создавать специальные массивы частиц, описывающих их покрытие, например, покрытие треугольниками. Тогда, при столкновениях сложных 3-х мерных тел, нужно постараться максимально точно вычислить обмены импульсами и моментами импульсов, исходя из законов сохранения импульса и момента импульса, чтобы не получались инерциоиды, как в некоторых компьютерных играх.
Если выписать формулы для искомых величин, то нужно численно решать довольно сложные системы дифференциальных уравнений. Зато как интересно! И полезно вывести оценку роста погрешности вычислений с ростом dt. В идеале dt - бесконечно малая величина, характеризующая непрерывный процесс. Но обычные компьютеры ориентированы на дискретные алгоритмы, где dt уже совсем не бесконечно малая...
Размышляю, как эти дифференциальные уравнения лучше численно решать.