Руст
juna
Если потерпите до понедельника, пришлю статью.
Добавлено спустя 1 минуту 48 секунд:
Győry, K.(H-AOS-NTR)
On the

conjecture in algebraic number fields.
Acta Arith. 133 (2008), no. 3, 281--295.
Let

be a number field. The radical of the triple
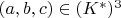
is defined as
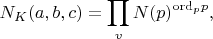
where

is the rational prime below
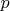
and the product is taken over all the finite places

such that
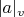
,
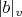
and
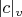
are not equal. The

conjecture asserts that the relative height
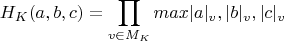
of any triple
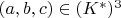
satisfying

cannot be too large compared with its radical. In the paper under review, the author shows a totally explicit estimate implying that, for every

, we have
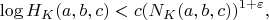
where

is an effectively computable positive constant which depends only on

and on

. Roughly speaking, he is essentially one logarithm away from establishing the uniform

conjecture in number fields, as formulated by D. W. Masser [Proc. Amer. Math. Soc. 130 (2002), no. 11, 3141--3150 (electronic); MR1912990 (2003d:11050)].
The theorems are deduced from recent explicit estimates concerning

-unit equations obtained by the author and K. Yu [Acta Arith. 123 (2006), no. 1, 9--41; and depend ultimately on the best known lower bounds for linear forms in logarithms of algebraic numbers.