Кажется удалось сделать еще шаг в понимании теоремы Ферма

[Мат]

Доказательство неразрешимости уравнения:
x^{2n}+y^{2n}=z^{2n},при n>1, n-простое (1)
1. Из чисел $x,y,z$ хотя бы два не делятся на n.
2. Допустим ни $z$, и ни $x$ не делятся на $n$. Тогда т.к. n-простое, для уравнения (1) справедливы разложения:
$z^{2n}=x^{2n}+y^{2n}=(x^2+y^2 )(x^{(2n-2)}-x^{(2n-4)} y^2+...-x^2 y^{(2n-4)}+y^{(2n-2)})$ (2)
$x^{2n}=z^{2n}-y^{2n}=(z^2-y^2 )(z^{(2n-2)}+z^{(2n-4)} y^2+...+z^2 y^{(2n-4)}+y^{(2n-2)})$ (3)
$y^{2n}=z^{2n}-x^{2n}=(z^2-x^2 )(z^{(2n-2)}+z^{(2n-4)} x^2+...+z^2 x^{(2n-4)}+x^{(2n-2)})$ (4)
где множители в правых частях (2), (3) и (4) – взаимно простые числа.
3. Для уравнения (4) справедливо также разложение:
$y^{2n}=z^{2n}-x^{2n}=(z+x)(z-x)(z^{(2n-2)}+z^{(2n-4)} x^2+...+z^2 x^{(2n-4)}+x^{(2n-2)})$ (5)
где множители в правой части также – взаимно простые числа.
4. Тогда уравнение (5) можно представить:
$y^{2n}=z^{2n}-x^{2n}=(z+x)(z-x)(z^{(2n-2)}+z^{(2n-4)}x^2+...+z^2x^{(2n-4)}+x^{(2n-2)})=y_0^{2n}y_1^{2n}y_2^{2n}$ (6)
5. Учитывая, что:
$(z+x)=y_0^{2n}$
$(z-x)=y_1^{2n}$ (7)
$(z^{(2n-2)}+z^{(2n-4)} x^2+...+z^2 x^{(2n-4)}+x^{(2n-2)})=y_2^{2n}$
6. Тогда попарно складывая первые два уравнения системы (7):
$2z=y_0^{2n}+y_1^{2n}$
$2x=y_0^{2n}-y_1^{2n}$ (8)
$2y=2y_0 y_1 y_2 $
7. Учитывая, что $(2x)^{2n}+(2y)^{2n}=(2z)^{2n}$ – также решение уравнения (1), получим:
$(y_0^{2n}-y_1^{2n} )^{2n}+(2y_0 y_1 y_2 )^{2n}=(y_0^{2n}+y_1^{2n} )^{2n}$
$(2y_0 y_1 y_2 )^{2n}=(y_0^{2n}+y_1^{2n} )^{2n}-(y_0^{2n}-y_1^{2n} )^{2n}$
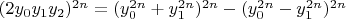
$(2y_0 y_1 y_2 )^{2n}=((y_0^{4n}+y_1^{4n} )+2y_0^{2n} y_1^{2n} )^n-((y_0^{4n}+y_1^{4n} )-2y_0^{2n} y_1^{2n} )^n$ (9)
Обозначим:
$(y_0^{4n}+y_1^{4n} )=p$
$2y_0^{2n} y_1^{2n}=q$ (10)
Тогда для (9) справедливо:
$(2y_0 y_1 y_2 )^{2n}=(p+q)^n-(p-q)^n=2np^{(n-1)} q+...+n(n-1) p^2 q^{(n-2)}+2q^n$
$(2y_0 y_1 y_2 )^{2n}=2np^{(n-1)} q+\frac{n(n-1)(n-2)}{3} p^{(n-3)} q^3+...+n(n-1) p^2 q^{(n-2)}+2q^n$ (11)
8. Т.к. левая часть (11) делится на $2^{2n}$, то и правая часть (11) делится на $2^{2n}$.
9. Если в уравнении (9) множители $y_0$ и $y_1$ разной четности, то в силу соотношения (10) p и q будут также разной четности, при этом:
$p=4k_1+1$
$q=4k_2$
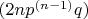
10. Но тогда, учитывая п.8 т.к. p – нечетно, то в правой части (11) $(2np^{(n-1)}q)$ делится на 2 в той же степени, что и $\frac{n(n-1)(n-2)}{3} p^{(n-3)}q^3$. Т.к. все остальные множители правой части содержат q в еще большей степени. Но это невозможно, т.к. p – нечетно.
Таким образом, ни в системе (8), ни в уравнении (9) числа $y_0$ и $y_1$ не могут быть разной четности.

[bot]

Цитата:

Кажется удалось сделать еще шаг в понимании теоремы Ферма

Чем мотивируется рассмотрение чётного показателя?
Вы бы лучше в эту сторону шаг сделали.

Предположим мы ещё не знаем, что ВТФ доказана, но нам стало известно, что для нечётного показателя она справедлива.

Приступаем к доказательству для $n=2^km$ с нечётным $m$ и $k>0$.

Пусть $x_0^n+y_0^n=z_0^n$ для некоторых положительных целых чисел $x_0, \ y_0, \ z_0$.

Тогда $(x_0^{2^k})^m+(y_0^{2^k})^m=(z_0^{2^k})^m$, то есть $X_0^m+Y_0^m=Z_0^m$ для $X_0=x_0^{2^k}, \ Y_0=y_0^{2^k}, \ Z_0=z_0^{2^k}$ - противоречие с нечётным случаем при $m>1$.
При $m=1$ получаем $x_0^{2^k}+y_0^{2^k}=z_0^{2^k} \iff (x_0^{2^{k-2}})^4+(y_0^{2^{k-2}})^4=(z_0^{2^{k-2}})^4$. В случае k>1 это даёт противоречие со случаем n=4, доказанным ещё самим Ферма.

Не сомневаюсь, что именно это рассуждение мотивировало Пьера Ферма на рассмотрение случая n=4, для затравки, так сказать.

[AD]

Цитата:

$z^{2n}=x^{2n}+y^{2n}=(x^2+y^2 )(x^{(2n-2)}-x^{(2n-4)} y^2+...-x^2 y^{(2n-4)}+y^{(2n-2)})$ (2)

Хотите сказать, что
$x^4+y^4=(x^2+y^2)(x^2-y^2)$

$n=2>1$ и простое.
Поправьте.

Добавлено спустя 4 минуты 48 секунд:

Мат в сообщении #168628 писал(а):

4. Тогда уравнение (5) можно представить:
$y^{2n}=z^{2n}-x^{2n}=(z+x)(z-x)(z^{(2n-2)}+z^{(2n-4)}x^2+...+z^2x^{(2n-4)}+x^{(2n-2)})=y_0^{2n}y_1^{2n}y_2^{2n}$ (6)
5. Учитывая, что:
$(z+x)=y_0^{2n}$
$(z-x)=y_1^{2n}$ (7)
$(z^{(2n-2)}+z^{(2n-4)} x^2+...+z^2 x^{(2n-4)}+x^{(2n-2)})=y_2^{2n}$

Правильно ли я понимаю, что пункт 5 - это определение $y_0$, $y_1$ и $y_2$? (Во всяком случае, они отсюда более-менее однозначно выражаются). И тогда почему вы дальше предполагаете, что они целые? Но это можно обойти, заменив словосочетание "$y_0$ четно" на "$y_0^{2n}$ четно" и т.п.

Добавлено спустя 10 минут 2 секунды:

Цитата:

$(z+x)=y_0^{2n}$
$(z-x)=y_1^{2n}$ (7)

Цитата:

Обозначим:
$(y_0^{4n}+y_1^{4n} )=p$
$2y_0^{2n} y_1^{2n}=q$ (10)

Цитата:

9. Если в уравнении (9) множители $y_0$ и $y_1$ разной четности, то в силу соотношения (10) p и q будут также разной четности, при этом:
$p=4k_1+1$
$q=4k_2$

$y_0^n$ и $y_1^n$ заведомо не могут быть разной четности просто по определению (потому что $z-x$ и $z+x$ имеют одинаковую четность). И это, видимо, уже доламывает рассуждение.

[Мат]

AD писал(а):

$q=4k_2$
$y_0^n$и $y_1^n$ заведомо не могут быть разной четности просто по определению (потому что $z-x$ и $z+x$ имеют одинаковую четность). И это, видимо, уже доламывает рассуждение.

не совсем так, подумайте лучше. Смысл не в том, что $z-x$ и $z+x$ одинаковой четности, смысл в том, что они не могут быть разной четности

[AD]

Цитата:

Смысл не в том, что $z-x$ и $z+x$ одинаковой четности, смысл в том, что они не могут быть разной четности

Ну так а я про что говорю? $z-x$ и $z+x$ не могут быть разной четности. Тривиально. Потому что $(z+x)-(z-x)=2x$ - четно. Так что все рассуждения, проведенные в предположении

Цитата:

Если в уравнении (9) множители $y_0$ и $y_1$ разной четности

бессмысленны.

[Мат]

Цитата:

Правильно ли я понимаю, что пункт 5 - это определение $y_0$, $y_1$ и $y_2$? (Во всяком случае, они отсюда более-менее однозначно выражаются).

Совершенно правильно, т.к.$y_0$, $y_1$, $y_2$ - взаимно простые числа, отсюда следует, что каждое из них является 2n-ой степенью некоего числа.

Добавлено спустя 1 минуту 26 секунд:

Цитата:

Тривиально.

Нет. Не тривиально. Думайте лучше

[AD]

Мат в сообщении #168674 писал(а):

Совершенно правильно, т.к.$y_0$, $y_1$, $y_2$ - взаимно простые числа, отсюда следует, что каждое из них является 2n-ой степенью некоего числа.

Почему это они взаимно просты? Из определения не слеудет даже, что они целые.

Мат в сообщении #168674 писал(а):

Нет. Не тривиально. Думайте лучше

Только что представил вам доказательство этого факта в полстрочки. Читайте внимательнее.

[Мат]

В разложениях (2), (3), (4) - одно число в левой части обязательно четно (один из членов уравнения (1)).
Тогда относительно данного разложения будут также справедливы п.4-10

[AD]

Краткое содержание последнего вашего сообщения: "у меня всё правильно, чё пристал ваще".

[Мат]

Цитата:

Почему это они взаимно просты? Из определения не слеудет даже, что они целые.

Это древнее утверждение. Можно найти в доказательстве самого Ферма для n = 4. Просто у меня сделано обобщение для степени порядка 2n.

[AD]

Еще раз.

Мат писал(а):

$(z+x)=y_0^{2n}$

Докажите, что существует целое число $y_0$, удовлетворяющее процитированному равенству.

Добавлено спустя 25 секунд:

Мат в сообщении #168679 писал(а):

Просто у меня сделано обобщение для степени порядка 2n.

Не вижу. Где сделано?

[Мат]

Цитата:

Не вижу. Где сделано?

В уме сделано. Я полагаю этот факт тривиален. Любой сколь угодно поверхностно знакомый с теорией чисел, должен быть знаком с ним. Но если это так необходимо, я приведу доказательство, хотя оно длинно

Добавлено спустя 3 минуты 32 секунды:

Смысл в том, что если числа $y_0$, $y_1$, и $y_2$ - не являются 2n-ми степенями, то они имеют общие множители. Тогда они не взаимно простые. Но это невозможно, т.к. z и x - взаимно простые.

Добавлено спустя 14 минут 16 секунд:

Мат писал(а):

В разложениях (2), (3), (4) - одно число в левой части обязательно четно (один из членов уравнения (1)).
Тогда относительно данного разложения будут также справедливы п.4-10

Так вот, если предположить, что y - четно, то в разложениях 6 -10 появится общий множитель 2 из которого будет следовать что и $z+x$ и $z-x$ - четно, но при этом $z+x$ и $z-x$ делятся на 2 в различных степенях. Т.е. $m_0(z-x)=2^k(z+x)m_1$. Откуда выйдет, что оба числа $z+x$ и $z-x$ в разложении (5) всегда будут четны. И третьего не дано. Но тогда не существует ни одного простого разложения - все разложения комбинированные. А это невозможно.

[bot]

Мой вопрос о мотивации игнорируется. Без мотивации лень даже ниже первой строчки опускаться. Это уже не первая тема о чётном показателе в теореме Ферма. Там я воздержался, а здесь не утерпел.

Зачем это нужно, если для решения проблемы Ферма чётный случай не имел никакого значения со времён самого Ферма?

В той теме появилось хоть какое-то объяснение. Оказывается автора интересует совсем другое уравнение и на теореме Ферма он типа инструментарий обтачивает, хм ... странно конечно, но хоть что то.

[Мат]

Цитата:

Чем мотивируется рассмотрение чётного показателя?

Трудностями в рассмотрении простых показателей

[AD]

Мат в сообщении #168682 писал(а):

Смысл в том, что если числа $y_0$, $y_1$, и $y_2$ - не являются 2n-ми степенями, то они имеют общие множители. Тогда они не взаимно простые. Но это невозможно, т.к. z и x - взаимно простые.

Не понятно. Почему не может быть так, что, скажем, $z-x$ делится на $p_1^{k_1}$, $x+z$ - на $p_2^{k_2}$, $p_1\neq p_2$, а третий длиннющий сомножитель - на $p_1^{2n-k_1}p_2^{2n-k_2}$?