Статитическая сумма БКА вывод

[Enceladoglu]

Хуанг, Статистическая Механика, Глава 7


У меня три вопроса
1) Я не понял почему в сумме $H(p,q,N) = H(q_1,p_1,N_1) + H(q_2,p_2,N_2) $ ф-я $H$ одна и та же, но вычисляется при разных аргументах в 7.24.
2) Не понял смысл суммы

$$\sum \frac{N!}{N_1!N_2!}$$

при вычислении статистической суммы 7.25

[amon]

Enceladoglu в сообщении #1684939 писал(а):

Я не понял почему в сумме $H(p,q,N) = H(q_1,p_1,N_1) + H(q_2,p_2,N_2) $ ф-я $H$ одна и та же, но вычисляется при разных аргументах в 7.24.

Это, конечно, ерунда, функции разные, отличающиеся хотя бы количеством аргументов, но на вывод это не влияет.

Enceladoglu в сообщении #1684939 писал(а):

2) Не понял смысл суммы

Частицы считаются неразличимыми. Поэтому состояния, отличающиеся только нумерацией частиц, следует считать эквивалентными и просуммировать по ним. $\frac{N!}{N_1!N_2!}$ - число способов выбрать $N_1$ частиц из $N$ одинаковых частиц (биномиальный коэффициент).

[Enceladoglu]

amon
Понял спасибо
Как я вначале сказал

Enceladoglu в сообщении #1684939 писал(а):

У меня три вопроса

Просто хотел уточнить правильно ли я понимаю написаное
The Г space for the grand canonical ensemble in spanned by all the canonical momontum and coordinates of system with 0,1,2.. number of particles (это третий абзац)
Т.е. БКА включает в себя системы с разным числом частиц, и фазовых координат по которым ведется интегрирование у нас всего $q_{11},p_{11};q_{21},p_{21}q_{22},p_{22};q_{31},p_{32}q_{32},p_{32};q_{33},p_{33},...$, тут первый индекс это кол-во частиц в системе ? Это относиться как к системе с в целом (но потом мы уточняем что кол-во частиц только N) так и отдельно к малой подсистеме

и что имеется ввиду под фразой through a change in the variables of integration if necesary ? (Эти слова прямо перед формулой 7.25). Это как раз про то что бы интегрировать по другим $q_{Nk},p_{Nk} $?

Наверное с первым индексом это я сильно загнул, но есть необходимость каждый раз добавлять новую переменную интегрирования

[Enceladoglu]

Вероятно я просто так и не понял саму идею вывода. Так сказано что система в целом рассматривается как просто канонический ансамбль, но почему ? Логично вроде предполагать что вся система изолирована и есть МКА, и из него уже пытаться вывести БКА так же как и КА, рассматривая малую подсистему.

[amon]

Enceladoglu в сообщении #1685376 писал(а):

Вероятно я просто так и не понял саму идею вывода.

Вывод в этом учебнике, на мой взгляд, весьма путанный. Гляньте, если интересно, в Климонтовича, " Статистическая физика". Там все это более последовательно выводится.

[Enceladoglu]

amon

amon в сообщении #1685382 писал(а):

Гляньте, если интересно, в Климонтовича

Я посмотрел, там какие-то непривычные обозначения, вероятно нужно читать раньше что там было.
Мне уже немного глупо менять книгу, раз я добрался до этого момента. Просто момент непонятный, мы считаем статистическую сумму для по факту микроканонического ансамбля.

Кстати, первое издание этой книги есть в переводе. Я просто взял второе, которое только в оригинале, в надежде что там будет более понятно (нет)

Enceladoglu в сообщении #1685387 писал(а):

Я посмотрел, там какие-то непривычные обозначения

Это был символ Кронекера, который обозначался буквой дельта. Крайне "непривычно"

[amon]

Если Климонтович не пошел, можете еще попробовать Румер, Рывкин. Термодинамика, статистическая физика и кинетика.

[Enceladoglu]

amon
Пока я ищу там соответствующий параграф, думайте Хуанга нужно забросить по причине кол-тва косяков на единицу параграфов ? Хотя я не уверен что это косяк, просто я не понимаю этот момент. Тут идея вывода совсем какая-то другая. Т.е. если верить тому что написано, есть большой большой термостат, он в равновесии с большой системой, внутри которой маленькая система_1 которую мы и исследуем. Возможно это как-то связанно с "эквивалентностью МКА и КА". Кстати я его взял ибо кто-то тут его рекомендовал когда-то

Мне бы если и менять, то на что-то максимально похожее по стилю изложения.

[amon]

Enceladoglu в сообщении #1685396 писал(а):

Пока я ищу там соответствующий параграф

§ 62. T-V-$\mu$ и T-P-N-распределения по моему изданию. А учебник надо подбирать такой, который легко читается. Содержание везде примерно одинаковое.

[drzewo]

мне когда-то статфизика Климонтовича очень нравилась

[Enceladoglu]

Я нашел довольно простой вывод в каких то pdf лекциях каких то немцев.
Еще у Киттеля есть довольно просто, но там вся книга на квантовой механике, ни слова о фазовом пространстве, хотя принцип абсолютно тот же.
Вывод там на основе МКА. Это конечно намного проще и понятней чем в этой книге

Но вообще я сегодня думал, и мне кажется я начинаю догадываться про идею автора.
Есть система 1, и система 2 побольше. Система 2 есть резервуар частиц для системы 1 (в принципе и тепла тоже).
Система 1 + 2 в целом находиться в контакте с каким то большим термостатом (просто потому что мы это рассматриваем как канонический ансамбль)
В этом подходе мы можем четко разделить резервуар частиц и резервуар тепла. Т.е. наша маленькая система отдельно в контакте с резервуаром тепла, и отдельно с резервуаром частиц (хотя опять же, резервуар частиц может и теплом обмениваться с системой).
Хотя в этом подходе получается что резервуар частиц может напрямую или посредством нашей системы обмениваться теплом с термостатом, но вот обмен частицами между резервуаром частиц и термостатом никогда не будет.
Выглядит как-то так

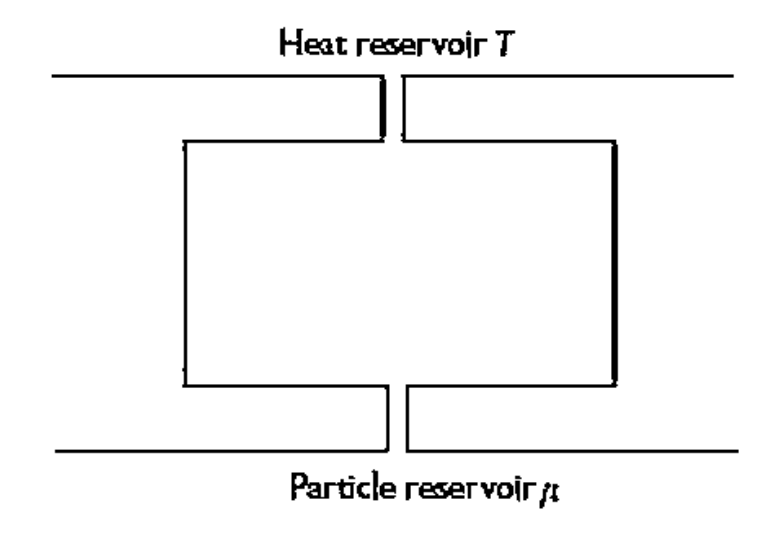
Тут бы еще стрелочки нарисовать - внизу обмен тепла и частиц, а вверху - только тепла
Если пытаться это выводить из микроканонического ансамбля, то у нас получается один общий резервуар для частиц и тепла.

Интересно, можно ли из этого подхода с каноническим ансамблем в каком-то пределе получить то же что и для подхода с микроканоническим ансамблем, т.е. что бы резервуар частиц и термостат совпал ?